احتمالاً شما هم به‌دفعات نام PID را شنیده‌اید، اما واقعاً PID چیست و به چه‌کار می‌آید؟ همراه ما باشید تا نگاهی بسیار دقیق به این کنترل‌کننده داشته باشیم.

آنچه که در این نوشتار خواهید خواند

• تعریف PID
• تاریخچه PID
• روش‌های کنترلی
• کنترل حلقه بسته یا باز
• عملکرد PID
• مدهای کنترلی PID
• انتخاب کنترل‌کننده مناسب
• تنظیم ضرایب PID
• سخت‌افزار PID
• کاربرد PID
• کنترلر دمای PID
• توسعه PID
• سؤالات متداول PID
• سخن پایانی
• منابع

امروز می‌خواهیم در ابتدا به تعریف PID و اینکه هر بخش از اسم آن به کدام مد کنترلی اشاره می‌کند بپردازیم در ادامه نگاهی به تاریخچه آن و نقش بی‌بدیل آقای نیکولاس مینورسکی در سال ۱۹۲۲ (۱۳۰۱ ه.ش) در توسعه PID خواهیم داشت. سپس قبل از اینکه وارد بحث اصلی شویم انواع روش‌های کنترلی را نام ببریم تا جایگاه دقیق PID بیشتر مشخص شود و پس آن در بخش عملکرد پی آی دی به عملکرد فانکشن‌های اساسی؛ تناسبی، انتگرالی و مشتقی اشاره کنیم.

ازآنجایی‌که PID خود از سه مد اصلی تشکیل شده است و هرکدام از این مدها علاوه بر عملکرد انفرادی می‌توانند با یکدیگر نیز مدهای جدیدی بسازند، به تمام ۵ مد موجود نگاهی خواهیم داشت و تاثیر هر مد را بروی خطا شرح خواهیم داد. پس از درک کامل آن به روش‌های انتخاب کنترل‌کننده مناسب می‌پردازیم تا شما با یک نگاه بتوانید کنترلر خود را انتخاب نمایید.

در تنظیم ضرایب PID، با اصطلاح Tune کردن آشنا خواهیم شد و سپس به سخت‌افزارهای موجود PID مانند؛ کنترلرهای اختصاصی، PLC و DCS می‌پردازیم.

ازآنجایی‌که کاربرد PID بیش از سایر کنترلرها می‌باشد در این بخش عمیق‌تر شده و علاوه بر مثال‌های مختلف به کنترلر دمای PID و مسائل مرتبط به آن خواهیم پرداخت. در نهایت در بخش توسعه PID به ترند روز این تجهیز یعنی PID فازی نگاهی کوتاه خواهیم داشت.

قبل از ورود به بررسی اجازه دهید کار را با دیدن یک کلیپ کوتاه در مورد معرفی PID شروع نماییم، بدین ترتیب شما را به دیدن این کلیپ کوتاه که توسط تیم PowerEn به فارسی ترجمه و زیرنویس شده است دعوت می‌نماییم.

فیلم (به‌زودی)

تعریف PID

کنترل‌کننده پی‌آی‌دی یا Proportional–Integral–Derivative یک سیستم کنترلی بر پایه فیدبک (بازخورد) می‌باشد که هدف اصلی آن نزدیک کردن نتیجه نهایی فرآیند به مقدار مدنظر ما می‌باشد. به زبان ساده‌تر، تمام دغدغه یک کنترل‌کننده PID، هدایت سیستم به‌طرف یک سطح، موقعیت و یا هر مقداری که ما مشخص می‌کنیم، می‌باشد.

PID کنترلرها در صنعت جزء دقیق‌ترین و پایدارترین کنترل‌کننده‌ها به‌حساب می‌آیند و عمدتاً از آنها در راستای خودکارسازی (یا بخشی از یک اتوماسیون) کارها برای نزدیک شدن (تا جای ممکن) به خروجی از پیش تنظیم شده یا هدفی مشخص استفاده می‌کنیم.

بیش از ۹۰% سیستم‌های کنترلی از PID به‌عنوان کنترل‌کننده بازخوردی استفاده می‌کنند^[1]

به‌خاطر عملکرد قوی و سادگی عملکردی، این روش توسط عمده شرکت‌های مطرح دنیا در زمینه ساخت کنترلر پذیرفته شده است و از آن در محصولات خود استفاده می‌کنند.

در کنترل‌کننده PID دو تعریف “خطا” و “SetPoint” از اهمیت بالایی برخوردار هستند. ست‌پوینت در اینجا به معنای نقطه مدنظر (سطح، موقعیت، کمیت و یا هر چیزی که ما می‌خواهیم در سیستم کنترلی به آن برسیم) می‌باشد و از طرف دیگر خطا به میزان انحراف (اختلاف) میان نقطه مدنظر و مقدار نهایی خروجی گفته می‌شود. نگفته پیداست که هرچه خطا کمتر باشد بهتر بوده و بدین معناست که ما توانسته‌ایم مقدار نهایی سیستم را با مقدار مدنظر خودمان دقیقاً یکی نماییم.

برای رسیدن به این نقطه مطلوب (خطا = صفر، مقدار خروجی سیستم = SetPoint) سیستم کنترلی PID از سه عملگر به نام‌های؛ تناسبی (Proportional)، انتگرال‌گیر (Integral) و مشتق‌گیر (Derivative) استفاده می‌کند. این سه ضریب پایه در هر کنترلر پی آی دی برای کاربردهای خاص به‌منظور رسیدن به واکنش بهینه متغیر هستند. در ادامۀ بحث به شکلی مفصل به این ضرایب و نحوه عملکرد آنها خواهیم پرداخت.

ضریب تناسبی باعث ایجاد یک کنترل صاف و بدون تغییرات شدید می‌گردد، ضریب انتگرالی به طور خودکار خطای سیستم را اصلاح می‌کند و درنهایت کنترل مشتق به‌سرعت به اختلالات پاسخ می‌دهد.

تاریخچه PID

اگر بخواهیم خیلی در تاریخ PID عمیق شویم به قرن ۱۷ خواهیم رسید، زمانی که از ابتدایی‌ترین گارونرها به‌عنوان یک کنترل‌کننده پیوسته استفاده می‌شد^[2] (دقت داشته باشید که PID کنترلر در دسته کنترل‌کننده‌های پیوسته قرار می‌گیرد).

به جهت کوتاه و مفید بودن این بخش از قرن ۱۷ عبور می‌کنیم و داستان را با آقای Elmer Ambrose Sperry محقق و کارآفرین آمریکایی که در سال ۱۹۱۱ (۱۲۹۰ ه.ش) بروی یک نمونه اولیه کنترل‌کننده PID جهت هدایت کشتی‌ها کار می‌کرد، شروع می‌کنیم.

ازآنجایی‌که آقای Elmer یک محقق تجربی بود تا یک ریاضی‌دان، به پیشرفت قابل‌توجهی نتوانست دست یابد تا اینکه در سال ۱۹۲۲ (۱۳۰۱ ه.ش) قوانین پایه و عملکردی PID که ما امروزه به‌عنوان مبنای عملکردی آنها می‌دانیم توسط دانشمند آمریکایی و روسی به نام نیکولاس مینورسکی تهیه شد.

مینورسکی پروژه تحقیق و طراحی فرمان اتوماتیک برای یک کشتی نیروی دریایی ایالات متحده بر اساس مشاهدات یک سکان‌دار را آغاز نمود. در این حین او متوجه شد که سکان‌دار کشتی نه‌تنها بر اساس خطای فعلی مسیر بلکه بر اساس خطای گذشته و همچنین نرخ لحظه‌ای تغییرات، کشتی را هدایت می‌کند.^[3] پس از آن مینورسکی به سراغ اثبات ریاضیاتی آن رفت، در عمل مینورسکی به دنبال ثبات بود نه کنترل عمومی و همین هدف باعث ساده‌سازی قابل‌توجهی در متد او گردید.

او دریافت که کنترل تناسبی (ضریب P در نام PID) می‌تواند ثبات را در برابر اغتشاشات کوچک فراهم نماید، در ادامه او برای حل مشکل وجود دائمی مقداری خطا، به انتگرال (ضریب I در نام PID) روی آورد که البته کافی نبود و سرانجام با افزودن مشتق‌گیر (ضریب D در نام PID) توانست به ثبات و بهبود مدنظر خود برسد.

در نهایت نیروی دریایی آمریکا سیستم بی‌نظیر مینورسکی را به دلیل مقاومت پرسنل به کار نگرفت!

بااین‌حال حرکت Nicolas Minorsky سرآغازی جدید برای سیستم‌های کنترلی به شمار می‌رود و پس از آن اندک‌اندک افراد بسیاری در این زمینه کار کردند و حتی نسخه پنوماتیکی PID نیز ساخته شد.

این مسیر تا جایی ادامه پیدا کرد که ما امروزه شاهد پیشرفته‌ترین و به‌نوعی کامل‌ترین نسخه کنترلر PID در عصر حاضر می‌باشیم.

روش‌های کنترلی

قبل از اینکه به بحث اصلی یعنی PID بپردازیم اجازه دهید نگاهی داشته باشیم به مهم‌ترین دسته‌بندی روش‌های کنترلی از دید “تولید فرمان”.

روش‌های کنترلی به دو دسته: پیوسته و گسسته تقسیم می‌شوند، هرکدام از این بخش‌ها نمایندگان ویژه‌ای دارند که در ادامه به آنها خواهیم پرداخت.

کنترل گسسته

در این بخش با عناصر گسسته سروکار داریم و به همین دلیل از جبر و حساب عمدتاً استفاده می‌شود. برای درک بهتر این واژه بهتر است متغیر گسسته را تعریف کنیم:

متغیر گسسته می‌تواند اعداد یا ارزش‌هایی را که مشخص‌کننده یک وجه مشخص و معیّن از یک مقیاس هستند، به خود اختصاص دهد. به‌عنوان‌مثال، جنس یک متغیر گسسته است: یک شخص یا زن است یا مرد. اختصاص هر نوع ارزش دیگری بین این دو نوع ارزش امکان‌پذیر نیست. تعداد بازیکنان یک تیم فوتبال نیز یک متغیر گسسته است، زیرا فقط امکان داشتن ۱، ۲، ۳، ۴، ۵، ۶، ۷، ۸، ۹، ۱۰، ۱۱ بازیکن وجود دارد و نه ۵.۵ نفر بازیکن.

دو روش بسیار کاربردی در این بخش عبارت‌اند از: کنترل ON/OFF و کنترل PWM.

روش ON/OFF

ساده‌ترین نوع کنترل یک فرآیند، به شکل کنترل دو وضعیتی یا اصطلاحاً ON/OFF است. کولرگازی‌های قدیمی یک مثال از این نوع کنترل هستند.

اگر خاطرتان باشد، این کولرها دارای یک ترموستات بودند که دمای محیط را اندازه می‌گرفت. فرض کنید می‌خواستیم دمای محیط روی ۱۸ درجه تنظیم شود. به‌محض اینکه دمای محیط از این مقدار بیشتر می‌شد کولر روشن می‌گردید و با تمام توان شروع به خنک‌کردن اتاق می‌کرد. بعد از آن که دما به کمتر از ۱۸ درجه می‌رسید کولر خاموش می‌شد و درواقع منتظر می‌ماند تا دوباره دمای اتاق بالا رود و دوباره کولر کار خود را با تمام توان انجام دهد. این روش اگرچه کارایی داشت و گرمای تابستان را برای خانواده قابل‌تحمل می‌کرد اما به‌خاطر اینکه فقط در دو حالت روشن و خاموش عمل می‌کرد، نمی‌توانست دما را روی یک عدد، ثابت نگه دارد و دما مرتباً حول آن عدد نوسان می‌کرد. علاوه بر اینکه به‌خاطر تعداد زیاد روشن و خاموش شدن کولر، عمر آن کم شده و به‌خاطر جریان بالای راه‌اندازی موتور، هزینه برق هم بسیار زیاد می‌شد. اگر بخواهیم نمودار این نوع کنترل را نمایش دهیم شکلی مانند شکل زیر ایجاد خواهد بود.

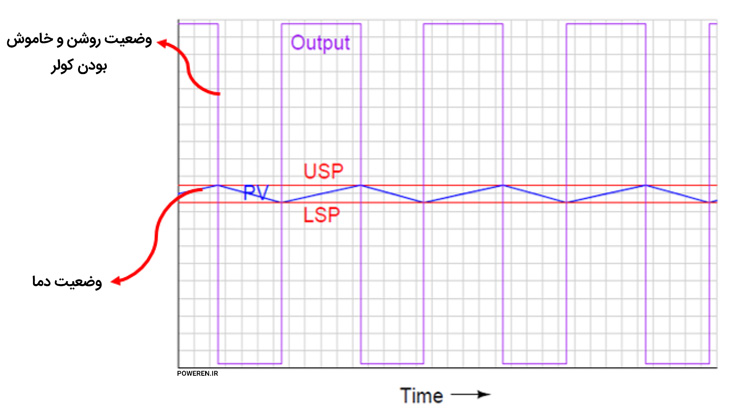
البته برای اینکه تعداد روشن و خاموش شدن‌ها را کاهش دهند از تکنیکی به اسم باند هیسترزیس استفاده می‌شود. مثلاً در مثال کولرگازی به‌جای آنکه بگویند دقیقاً کولر در دمای بالای ۱۸ درجه در سرویس قرار بگیرد و به‌محض رسید به ۱۸ از سرویس خارج شود، یک محدوده‌ای مثلاً ۲ درجه را در نظر می‌گیرند. به این صورت که کولرگازی در دمای 20 درجه در سرویس قرار می‌گیرد و بعد ازآنکه به ۱۸ رسید فوراً خاموش نمی‌شود بلکه اجازه می‌دهد بازهم دما کاهش‌یافته و به ۱۶ درجه برسد و آنگاه خاموش می‌شود. با این روش بااینکه تعداد خاموش و روشن‌های کولر کمتر است اما نوسان دمای خروجی بیشتر خواهد شد.

روش PWM

اگر بخواهیم یک مفهوم آنالوگ یا پیوسته را به‌وسیله یک موج صرفاً صفر و یک ایجاد کنیم از این نوع کنترل استفاده می‌کنیم. درواقع PWM رابط بین دنیای دیجیتال و آنالوگ است. برای این کار زمان صفر و یک شدن به‌گونه‌ای تنظیم می‌شود که درنهایت میانگین این صفر و یک شدن‌ها مقدار مطلوب را به دست دهد. مثلاً اگر زمان یک بودن ۲ ثانیه و زمان صفر بودن ۸ ثانیه باشد، در یک دورهٔ ۱۰ ثانیه‌ای درواقع یک‌پنجم زمان که معادل یک موج با اندازه ۰.۲ است برای ما تولید می‌شود.

یکی از کاربردهای مهم تکنیک PWM استفاده از آن در اینورتر و درایوهای الکتریکی می‌باشد.

از همین روش برای تولید موج‌های متناوب هم می‌توان استفاده کرد. شکل زیر چگونگی تولید یک موج سینوسی را با استفاده از روش PWM توضیح می‌دهد.^[4]

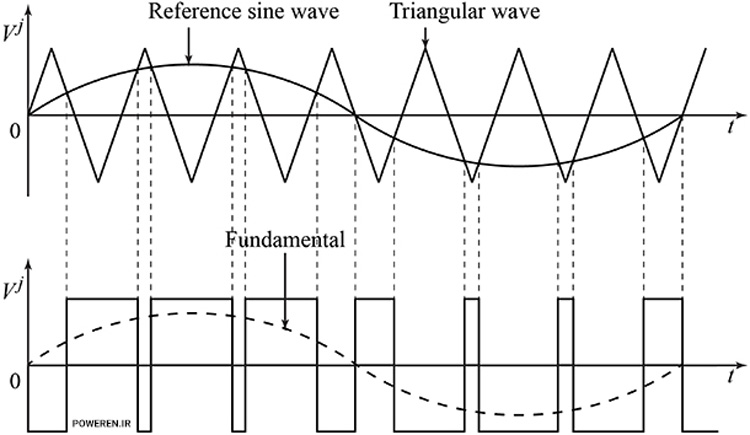
کنترل پیوسته

این روش به شکلی غیرمستقیم در مقابل نوع گسسته که صحبت شد قرار گرفته است. در نوع پیوسته عمدتاً از توابع مثلثاتی، مشتق و انتگرال استفاده می‌شود. برای درک بهتر این واژه نیز بهتر است متغیر پیوسته را تعریف کنیم:

متغیر پیوسته متغیری است که بین دو واحد آن هر نقطه یا ارزشی را می‌توان انتخاب کرد. در این متغیر درجات مختلف اندازه‌گیری وجود دارد و دقت وسیله اندازه‌گیری، تعداد این درجات را تعیین می‌کند. به‌عنوان‌مثال، وزن یک متغیر پیوسته است و می‌تواند بین صفر تا بی‌نهایت باشد. وزن یک شخص می‌تواند ۵۵ یا ۵۶ کیلوگرم باشد و یا می‌تواند هر عددی بین این دو عدد باشد (مثلاً ۵۵.۶ یا ۵۵.۶۴ کیلوگرم). قد، زمان، طول یا ارتفاع پرش، درصد چاقی بدن، و سطح هموگلوبین خون نمونه‌هایی از متغیرهای پیوسته هستند.

در این بخش نماینده ما، PID قرار گرفته است که با یک مثال سعی می‌کنیم با آن بهتر آشنا شوید.

روش PID

فرض کنید یک کتری را روی گاز گذاشته‌اید و می‌خواهید دمای آب داخل آن را روی 70 درجه نگهدارید. یک روش این است که وقتی دمای آب کمتر از 70 درجه شد شعله گاز را تا آخر زیاد کنید و هروقت دما بیشتر شد شعله را خاموش کنید که در این صورت دما احتمالاً خیلی زیاد شده و سپس کم می‌شود. روش دیگر (PID) آن است که باتوجه‌به سرعت گرم‌شدن آب درون کتری و مقدار دمای فعلی آب، مقدار شعله را تنظیم کنید. مثلاً زمانی که آب 20 درجه است شعله را تا آخر زیاد کنید و بعدازاین که دما به حدود 50 درجه رسید آرام‌آرام شعله را کم کنید تا سرعت افزایش دما کمتر شود. در این حالت دمای آب به شکل مناسب‌تری به مقدار مطلوب خواهد رسید.

در بخش بعدی در PID دقیق‌تر خواهیم شد و به نحوه عملکرد آن خواهیم پرداخت، قبل از اینکه به سراغ این بخش برویم مجدداً خاطرنشان می‌شود که PID یک کنترلر حلقه بسته است.

کنترل حلقه بسته یا باز

برای دستیابی به کنترل دقیق‌تر، پارامتر تحت کنترل باید اندازه‌گیری شده و با ورودی مرجع مقایسه شود و سیگنال تحریکی متناسب با تفاضل ورودی و خروجی به سیستم اعمال شود. در نتیجه خطا تصحیح می‌شود. سیستمی با یک یا چند مسیر فیدبک مانند شکل زیر، یک سیستم حلقه بسته نامیده می‌شود.

به‌عنوان‌مثال اگر ما پمپی داشته باشیم که بخواهیم در خروجی‌اش، فشار آب ثابتی را به ما بدهد، می‌توانیم سرعت اینورتر روی آن را به‌صورت دستی روی مقدار ثابتی قرار دهیم و امیدوار باشیم که فشار در تمامی لحظات روی مدار ثابت بماند، و شب‌ها هم می‌توانیم کمی سرعت اینورتر را کم کنیم. این یک کنترل حلقه باز است.

راه‌حل بهتر به‌کارگیری یک سنسور فشار و اتصال سیگنال آن به اینورتر است. اینورتر مقدار واقعی (یعنی اندازه‌گیری شده) فشار را با مقدار مطلوب (نقطه مرجع موردنظر) مقایسه می‌کند و سرعت پمپ را دائماً تغییر می‌دهد تا فشار را در مقدار ثابتی نگه دارد. ازآنجاکه اتصال سنسور فشار یک حلقه تشکیل می‌دهد (اینورتر – موتور – پمپ – سنسور) این سیستم‌ها به سیستم‌های کنترلی حلقه بسته شهرت دارند. مقایسه این دو نوع کنترل در تصویر زیر آمده است.

کنترل حلقه بسته کاربردهای زیادی دارد، از سیستم‌های تثبیت‌کننده هواپیما گرفته تا کنترل تنش در سیستم‌های سیم‌پیچی، و همچنین کاربردهای ساده‌تری مثل تثبیت فشار، سرعت جریان یا دما.

مسئله مهم در کنترل حلقه بسته، پایداری است. در این سیستم با پردازش صحیح خطا می‌توان پایداری را ایجاد کرد. خط اتلاف بین نقطه مرجع و مقدار واقعی، سیگنال فیدبک یا اندازه‌گیری است. درنهایت خطا به سیستم کنترلی داده می‌شود که در مثال بالا همان اینورتر است. اینورتر باید بتواند با پردازش سریع خطای موجود را پردازش و برطرف کند.

عملکرد PID

همان‌طور که قبلاً گفته شد PID از سه جز بسیار مهم به نام‌های Proportional (تناسبی)، Integral (انتگرال‌گیری) و Derivative (مشتق‌گیری) تشکیل شده است. در عمل هرکدام از آن‌ها سیگنال خطا را به‌عنوان ورودی گرفته و عملیاتی را روی آن انجام می‌دهد و در نهایت خروجی‌شان با هم جمع می‌شوند. خروجی این مجموعه که همان خروجی کنترل‌کننده PID است برای اصلاح خطا (Error) به سیستم بازگشت (فیدبک) داده می‌شود.

برای اینکه با معادلات PID هم آشنا شویم دو فرمول استاندارد و تابع تبدیل آن را در زیر آورده‌ایم.

فرمول استاندارد PID به شکل زیر است:

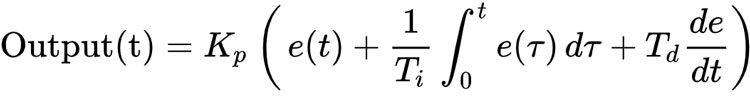
باتوجه‌به فرمول بالا به‌راحتی می‌توان تابع تبدیل زیر را به دست آورد:

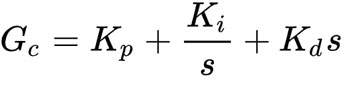
درنهایت اگر سه بخش را به‌صورت موازی در کنار هم قرار دهیم به دیاگرام کلی کنترلر PID، طبق شکل زیر خواهیم رسید.

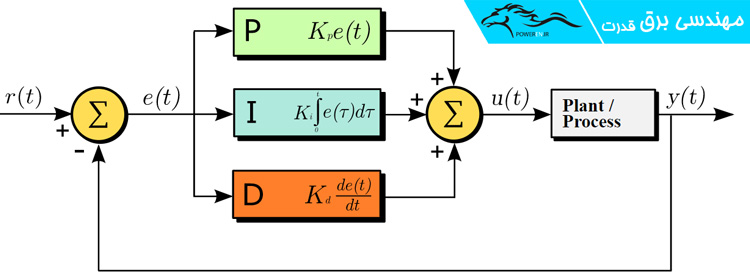
قاعده اساسی پشت عملکرد یک کنترل‌کننده PID این است که عبارت‌های تناسبی، انتگرالی و مشتقی باید به طور جداگانه تنظیم یا «کوک» شوند. این تنظیم توسط مهندس برق مربوطه و با تحلیل و عمدتاً آزمون‌وخطا به دست می‌آید.

جهت رسیدن به بهترین نقطه عملکردی PID باید مقدار هرکدام از ضرایب (P، I و D) را در کنار هم محاسبه کرده و درنهایت بهترین مقادیر را استفاده نمود

اینکه هرکدام از این ضرایب در کنترل PID چه نقشی دارند و اصولاً چگونه باید تعیین شوند را در بخش بعدی شرح خواهیم داد.

مدهای کنترلی PID

در کنترل‌کننده PID ۵ مد اساسی به نام‌های زیر داریم:

1. کنترل تناسبی (Proportional Controler)
2. کنترل انتگرالی (Integral Controler)
3. کنترل مشتقی (Derivative Controler)
4. کنترل تناسبی + انتگرالی (Proportional Integral Controller)
5. کنترل تناسبی + انتگرالی + مشتقی (Proportional Integral Derivative Controller)

هر یک از این ۵ مد، واکنش متفاوتی نسبت به خطا دارند. مقدار پاسخ تولیدی هر مد کنترلی را می‌توان با تغییر تنظیمات آن بهینه نمود و در نهایت با در کنار هم قراردادن (سه مد کنترلی اصلی؛ P، I و D) آن به یک سامانه بهینه PID دست یابیم. در ادامه، هر یک از این مدها را به‌صورت کامل بررسی می‌کنیم.

مد کنترل تناسبی (P)

در مد کنترل تناسبی خروجی کنترل‌کننده در تناسب با مقدار خطاست (به همین دلیل به آن تناسبی می‌گویند). اگر خطا بزرگ باشد، خروجی کنترل‌کننده هم بزرگ است و اگر خطا کوچک باشد خروجی کنترل‌کننده هم کوچک است.

تمام ضرایب PID یک مقدار بهینه دارند و به این صورت نمی‌باشد که صرفاً مقادیر آنها تا حد ممکن کم و یا زیاد نماییم.

پارامتر قابل تنظیم کنترل تناسبی، بهره کنترل‌کننده (Controller Gain) یا K_c نامیده می‌شود. هرچه بهره کنترل‌کننده بزرگ‌تر باشد، عمل کنترل تناسبیِ خطا را افزایش می‌دهد. اگر بهره کنترل‌کننده در مقدار بسیار بالایی تنظیم شود، حلقه کنترل شروع به نوسان می‌کند و ناپایدار می‌شود. از سوی دیگر، اگر بهره بسیار کم باشد، پاسخ به اغتشاشات یا تغییرات نقطه تنظیم، به‌اندازه کافی کارساز نخواهد بود.

معادله و شکل زیر گویای این وضعیت است:

P = K_c * E

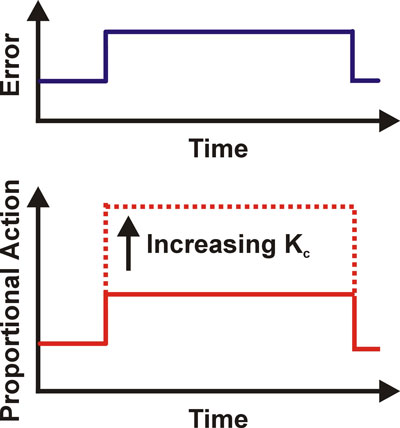
بخش P در کنترلر PID بر مدهای کنترل انتگرالی و مشتقی نیز تأثیر می‌گذارد. به همین دلیل است که این پارامتر را بهره کنترل‌کننده می‌نامیم، نه صرفاً بهره تناسبی.

درحالی‌که اغلب کنترل‌کننده‌ها از بهره کنترل‌کننده (K_c) به‌عنوان تنظیم تناسبی استفاده می‌کنند، برخی کنترل‌کننده‌ها از باند تناسبی (Proportional Band) یا PB بهره می‌برند که برحسب درصد بیان می‌شود.

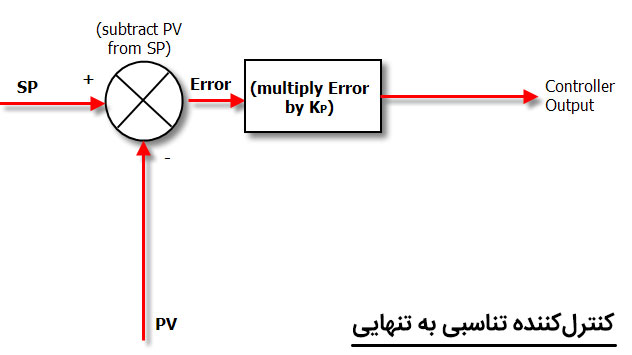
استفاده از کنترل‌کننده تناسبی به‌تنهایی، یک عیب بزرگ دارد و آن، آفست (Offset) است. آفست، یک خطای پایدار است که نمی‌توان به‌تنهایی با کنترل تناسبی آن را از بین برد.

برای درک بهتر آفست (Offset) اجازه دهید یک مثال کاربردی را باهم مرور نماییم:

تصور کنید که ما یک اتاق به همراه یک گرم‌کننده داریم، سیستم کنترلی ما در اینجا صرفاً بخش تناسبی (P) بوده و خبری از I و D فعلاً نیست.

در این اتاق دمای مدنظر باید بروی ۳۰ درجه سانتی‌گراد تنظیم شود.

گزاره بالا نقطه هدف و یا آنچه که ما می‌خواهیم می‌باشد، در ادامه شرایطی رخ می‌دهد که باهم واکنش کنترل‌کننده تناسبی را خواهیم دید.

۱. اتفاقی غیرمعمول می‌افتد و یکی از پنجره‌‌ها باز می‌شود.

۲. دمای اتاق به یکباره از ۳۰ به ۲۵ درجه می‌رسد و این کاهش با یک سرعت مشخص ادامه پیدا می‌کند.

۳. کنترل‌کننده تناسبی که از فیدبک دمای اتاق استفاده می‌کند متوجه تغییرات دمایی شده و سعی می‌کند با روشن‌کردن دمنده مانع این تغییر دمای ناخواسته شود.

۴. دمای اتاق به ۲۳ درجه رسیده ولی باتوجه‌به روشن شدن دمنده سرعت کاهش دما کمتر شده است.

۵. کنترل‌کننده تناسبی ما قدرت دمنده را افزایش می‌دهد.

۶. در این نقطه دقیقاً دمنده ما به همان اندازه که هوای سرد وارد اتاق می‌شود گرما تولید می‌کند پس دمای اتاق دقیقاً بروی عدد ۲۳ درجه Set می‌گردد.

۷. از دید کنترل‌کننده تناسبی تغییرات ناخواسته دما به اتمام رسیده و اکنون سیستم بدون هیچ خطایی در حال کار می‌باشد!

احتمالاً الان متوجه مشکل بزرگ استفاده از کنترل‌کننده تناسبی به‌تنهایی شده‌اید، درواقع این کنترل‌کننده پس از اتمام کار یک مقدار خطای دائمی در سیستم ایجاد می‌کند (اختلاف دمای ۳۰ درجه مدنظر با دمای کنونی اتاق که ۲۳ درجه سانتی‌گراد می‌باشد)، به این میزان خطای پایدار که در این مثال ۷ درجه سانتی‌گراد می‌باشد آفست (Offset) می‌گویند.

در کنترل فقط تناسبی، آفست تا زمانی که اپراتور به‌صورت دستی بایاس خروجی کنترل‌کننده را تغییر ندهد، وجود خواهد داشت. این کار معمولاً با قراردادن کنترل‌کننده در حالت دستی و تغییر خروجی به‌صورت دستی تا رسیدن به خطای صفر انجام می‌شود. پس از آن، کنترل‌کننده به حالت خودکار سوئیچ می‌شود. در این حالت می‌گوییم اپراتور به‌صورت دستی کنترل‌کننده را بازنشانی کرده است.

ضریب کنترلی در این مد K_p می‌باشد.

باتوجه‌به توضیحاتی که داده شد استفاده منفرد از کنترل‌کننده تناسبی عمدتاً جوابگوی کار ما نیست به همین دلیل به سراغ جزء دوم یعنی کنترل‌کننده انتگرالی می‌رویم.

مد کنترلی انتگرالی (I)

باتوجه‌به مشکل ذکر شده در بخش کنترل تناسبی و حذف انحراف همیشگی آن، از عملکرد انتگرال استفاده می‌شود.

I، انتگرال (نسبت به زمان) مقدار واقعی خطا است، به سبب انتگرال‌گیری، مقدار خطای بسیار کمی، پاسخ انتگرالی بسیار بزرگی را نتیجه می‌دهد. در ادامه عملیات کنترل‌کننده انتگرالی تا جایی ادامه می‌یابد تا خطای آفست صفر شود.

مد کنترل انتگرالی، خروجی کنترل‌کننده را به‌صورت پیوسته کم یا زیاد می‌کند تا خطا را به صفر کاهش دهد. اگر خطا بزرگ باشد، مد انتگرالی خروجی کنترل‌کننده را به‌سرعت افزایش یا کاهش می‌دهد و اگر خطا کوچک باشد، تغییرات آرام‌تر رخ خواهد داد.

به زبان ساده‌تر در عملکرد انتگرال، سطح زیر منحنی خطا، انتگرال منحنی خطاست. ازاین‌رو هرچند در عملکرد تناسبی، منحنی خطا دارای انحراف است، ولی چنانچه عملکرد انتگرال را به آن بیفزاییم به‌مرور سطح زیر منحنی خطا (هرچند که خطا کم باشد) زیاد می‌شود و این امر باعث افزایش سیگنال خروجی از کنترل‌کننده و کاهش مقدار خطا و انحراف می‌گردد.

کنترل‌کننده انتگرالی برای تغییرات سریع مناسب نیست و اگر در تجهیزی (مانند موتور الکتریکی) انتگرال‌گیری ذاتی وجود دارد بهتر است از این جز استفاده نشود.

ضریب کنترلی در این مد K_i می‌باشد.

در این بخش نیز به کنترل‌کننده انتگرالی منفرد (یعنی تنها از I برای کنترل استفاده نماییم) پرداختیم، در بخش بعدی به سراغ جزء D یا کنترل‌کننده مشتقی می‌رویم.^[5]

مد کنترلی مشتقی (D)

همین ابتدا خاطرنشان می‌شود که کنترل‌کننده مشتق‌گیر هیچ‌گاه به‌تنهایی استفاده نمی‌شود چون اگر خطا ثابت (غیر صفر) باشد، خروجی کنترل‌کننده صفر خواهد شد. در این وضعیت، کنترل‌کننده مانند حالت خطای صفر رفتار می‌کند، اما درواقع مقداری خطا (ثابت) وجود دارد.

y(t) ∝ de(t)/dty(t) = K_d * de(t)/dt

همان‌طور که در رابطه بالا نشان‌داده‌شده است، خروجی کنترل‌کننده مشتق‌گیر رابطه مستقیمی با سرعت تغییر خطا نسبت به زمان دارد. با حذف علامت تناسب، ما به ثابت بهره مشتق (K_d) می‌رسیم. به‌طورکلی کنترل‌کننده‌های مشتق‌گیر زمانی استفاده می‌شوند که متغیرهای فرآیند شروع به نوسان کنند یا تغییرات در سرعت بسیار بالا داشته باشند. کنترل‌کننده‌های مشتقی همچنین برای پیش‌بینی عملکرد آینده خطا، به‌وسیلهٔ منحنی خطا استفاده می‌شوند.

این نوع کنترل‌کننده در کنترل فرآیند نسبت به نویز بسیار حساس است و عمدتاً تنظیم با استفاده از سعی و خطا را دشوارتر می‌کند.

در این مد وقتی تغییرات خطا زیاد باشد، مد مشتقی عمل کنترل بیشتری تولید خواهد کرد. وقتی خطا تغییر نکند، عمل مشتقی صفر خواهد بود. مد مشتقی یک تنظیمات قابل تغییر دارد که زمان مشتق (T_D) نامیده می‌شود. هر چه زمان مشتق بیشتر باشد، عمل حاصل از مشتق بیشتری تولید خواهد شد. وقتی زمان مشتق بسیار طولانی باشد در این مد نیز نوسان‌هایی رخ می‌دهد و حلقه کنترل ناپایدار خواهد شد.

ضریب کنترلی در این مد K_d می‌باشد.

کنترل تناسبی + انتگرالی (PI)

از میان موارد بالا که تاکنون صحبت شد تنها شماره ۱ (کنترل‌کننده تناسبی) کاربردی می‌باشد، باقی موارد عمدتاً به‌صورت منفرد در جایی استفاده نمی‌شوند.

اگر کنترل‌کننده تناسبی را با کنترل‌کننده انتگرالی ترکیب نماییم به یک کنترل‌کننده جدید دست خواهیم یافت که دیگر مشکل آفست (OffSet) یا خطای ماندگار را نخواهد داشت. در شکل زیر دیاگرام این کنترل‌کننده کاربردی ترسیم شده است.

++ عکس دیاگرام PI کنترلر

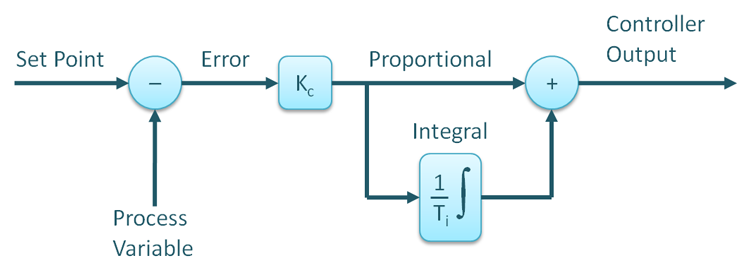
به این کنترلر به‌اختصار PI کنترلر می‌گویند.

اگر بخواهیم این کنترلر را به‌صورت رابطه ریاضی بیان نماییم به‌صورت زیر خواهد بود:

y(t) ∝ [e(t) + ∫ e(t) dt] y(t) = k_p *e(t) + k_i ∫ e(t) dt

در این کنترلر سطح زیر منحنی خطا را انتگرال منحنی خطا می‌دانند. ازاین‌رو هرچند در عملکرد تناسبی، منحنی خطا دارای انحراف است، ولی چنانچه عملکرد انتگرال را به آن بیفزاییم به‌مرور سطح زیر منحنی خطا زیاد می‌شود و این امر باعث افزایش سیگنال خروجی از کنترل‌کننده و کاهش مقدار خطا و انحراف می‌گردد.

تصویر زیر به‌خوبی نمایانگر تاثیر افزودن بخش انتگرال به بخش کنترل تناسبی می‌باشد و همان گونه که مشاهده می‌کنید سبب حذف کامل خطای ماندگار شده است.

کنترل تناسبی + انتگرالی + مشتقی (PID)

نگفته پیداست که این کنترل‌کننده ترکیب کنترل‌کننده‌های P، I و D است. خروجی کنترل‌کننده مجموع پاسخ‌های تناسبی، انتگرالی و مشتقی است.

چنانچه گفته شد عملکرد انتگرال به گذشته نظر دارد. برای افزودن آینده‌نگری به سیستم کنترل، عملکرد مشتق به دو عملکرد یاد شده اضافه می‌شود. مشتق یک منحنی در یک نقطه (در اینجا منحنی خطا)، ضریب زاویه یا میل به آینده منحنی را در آن نقطه نشان می‌دهد. ازاین‌رو می‌توان در فرآیندهایی که در آنها جرم زیادی باید شتاب داده شوند یا شتابشان کم شود و یا گرم یا سرد شوند از آنها استفاده کرد.

اگر بخواهیم PID را به شکل معادله ریاضی نشان دهیم به‌صورت زیر خواهد بود:

y(t) ∝ [e(t) + ∫ e(t) dt + de(t)/dt] y(t) = k_p * e(t) + k_i ∫ e(t) dt + k_d * de(t)/dt

در این معادله هر سه ضریب؛ K_p، K_i و K_d تأثیرگذار هستند.

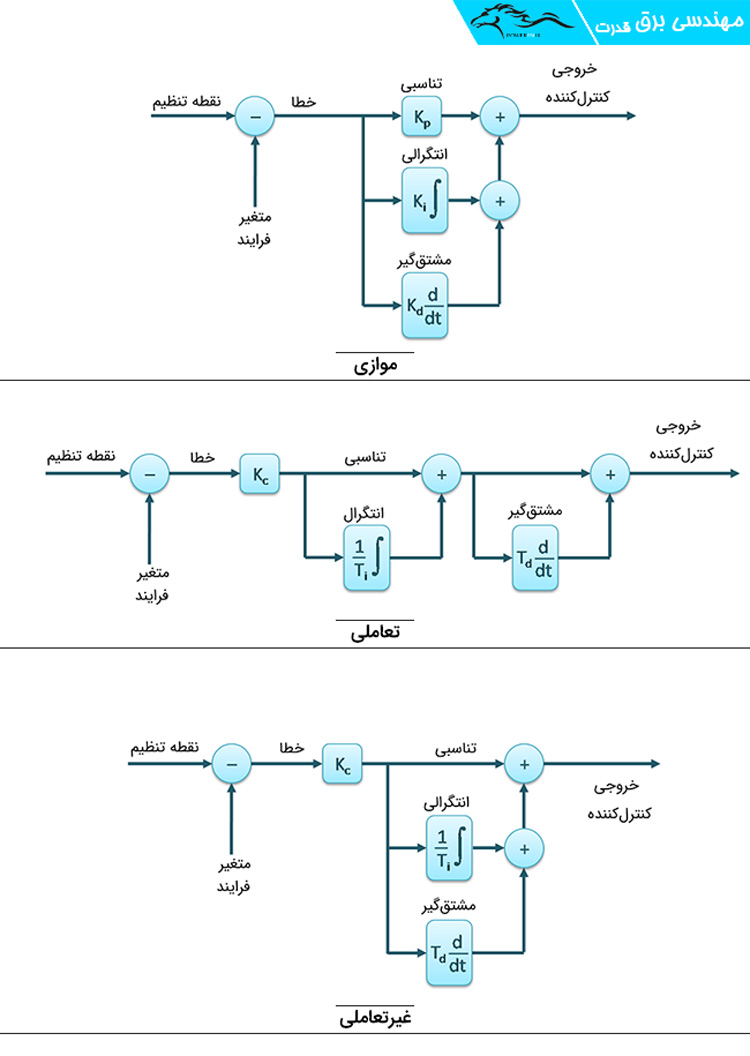
ازآنجایی‌که در ترکیب کردن دست ما باز است به همین دلیل برای این مد کنترلی سه پیکربندی ارائه شده است که عبارت‌اند از؛

• PID تعاملی (Interactive)
• PID غیرتعاملی (Noninteractive)
• PID موازی (Parallel)

در عمده کتاب‌‌ها و مقالات علمی از نوع PID موازی بیشتر استفاده می‌شود، با این وجود برخی از شرکت‌‌ها اجازه تنظیم و انتخاب نوع پیکربندی PID را نیز در اختیار اپراتور قرار می‌دهند.

در تصویر زیر به‌خوبی می‌توانیم به کیفیت عملکردی PID نسبت به چهار متد دیگر پی ببریم، در این شکل ۴ موج ترسیم شده است. موج اول سیگنال کنترل نشده است که دارای خطای فاحش و البته پایدار می‌باشد.

موج بعدی از کنترلر، تناسبی بوده و همان‌طور که انتظار می‌رفت بخش آفست آن دارای مقدار خطای ثابت می‌باشد. اگر موج کنترل‌کننده PI را با موج P مقایسه کنیم مشاهده می‌شود که به دلیل حضور المان انتگرال‌گیر بخش خطای ماندگار حذف شده است.

در نهایت موج PID قرار گرفته است که به دلیل حضور مشتق‌گیر توانسته‌ایم از نوسانات زیاد نسبت به PI جلوگیری نماییم.

در Gif (تصاویر متحرک) زیر به‌خوبی تاثیر هرکدام از ضرایب کنترل‌کننده‌‌ها به تصویر کشیده شده است، در این تصویر به راحتی می‌توان کارآمد بودن ترکیب؛ تناسب + انتگرال + مشتق را مشاهده کرد.

انتخاب کنترل‌کننده مناسب

تاکنون در مورد انواع مدهای کنترلی صحبت کردیم اما برای اینکه جمع‌بندی کنیم و درنهایت به‌سادگی بتوانیم تشخیص دهیم که کدام متد کنترلی برای ما مناسب است در ادامه توضیحاتی را ارائه خواهیم داد.

اولویت نخست ما در طراحی یک کنترل‌کننده، سادگی آن است هرچند ممکن است مقداری خطا هم به وجود بیاید! پس ممکن است در مواردی متد کنترلی P جایگزین PI و حتی PID باشد!

P: زمانی استفاده می‌شود که وجود آفست در سیستم مهم نبوده و قابل‌تحمل باشد یا وقتی‌که فرآیند به طور طبیعی دارای ماهیت انتگرالی باشد.

PI: زمانی استفاده می‌شود که آفست قابل‌تحمل نیست و باید در حالت ماندگار هیچ‌گونه خطای وجود نداشته باشد.

PD: اصولاً به‌ندرت استفاده می‌شود به همین دلیل در دسته‌بندی بالا آن را قرار نداده‌ایم. به‌کارگیری PD باعث خواهد شد که سیستم کنترلی با وجود مقادیر بزرگ‌تر بهره کنترل‌کننده، همچنان پایدار باقی بماند.

PID: زمانی که جبران برخی لختی‌‌های طبیعی در سرتاسر سیستم مهم باشد و سیگنال‌‌های فرآیند نسبتا عاری از نویز باشند قطعا PID انتخاب ما خواهد بود.

در جدول زیر مزایا و معایب سه کنترل‌کننده اصلی آورده شده است.

++جدول مزایا و معایب کنترل‌کننده‌‌های P، I و D

ضریب	مزایا	معایب
P	سریع ساده و ارزان می‌باشد.	نمی‌تواند خروجی را به مقدار نهایی مطلوب برساند. تصمیمات بر اساس خطای لحظه‌ای است.
I	می‌تواند خروجی را به مقدار مطلوب برساند. به نویز یا تغییرات ناگهانی حساس نیست. بر اساس تاریخچه خطا عمل می‌‌کند.	خیلی کند است. پایداری سیستم را کاهش می‌دهد. ساده و ارزان نیست.
D	خیلی سریع است. سیستم را پایدار می‌کند.	نمی‌تواند خروجی را به مقدار نهایی برساند. به نویز حساس است. ساده و ارزان نیست.

تنظیم ضرایب PID

یکی از مهم‌ترین نکاتی که باید قبل از تنظیم ضرایب PID بدانید این است که اصولاً تغییر هر پارامتر، باعث چه تغییراتی در منحنی سیستم کنترل خواهد شد. جدول زیر تأثیر هرکدام از این پارامترها را بر منحنی سیستم نشان می‌دهد:

ضریب	زمان صعود (Rise time)	بالازدگی (Overshoot)	زمان نشست (Setting time)	خطای حالت ماندگار (Steady error)
Kd	کاهش	کاهش	کاهش	تغییر کوچک
Kp	کاهش	افزایش	تغییر کوچک	کاهش
Ki	تغییر کوچک	افزایش	افزایش	حذف

تنظیم ضرایب PID یا اصطلاحاً Tune کردن این ضرایب روش‌های گوناگونی دارد و در بسیاری از اوقات باتوجه‌به شناختی که فرد با تأثیر ضرایب و همین‌طور رفتار فرآیند دارد، به‌صورت تجربی و گاهی آزمون‌وخطا انجام می‌شود. همچنین امروزه بسیاری از کنترلرهای دیجیتال از ویژگی به نام Auto tune برخوردار هستند که به‌صورت خودکار ضرایب مناسب را بعد از چند بار امتحان به دست می‌آورد.

باتوجه‌به اینکه این بخش نیاز به مباحث دیگری دارد سعی خواهیم کرد بررسی روش‌های تنظیم ضرایب PID را در آینده و در مطلبی جداگانه آموزش دهیم.

سخت‌افزار PID

قدیمی‌ترین سخت‌افزار ساخته شده همان گونه که در بخش تاریخچه گفته شد، PIDهای پنوماتیکی می‌بودند که امروزه به دلیل حضور الکترونیک و الکترونیک قدرت عملاً کنار گذاشته شده‌اند، به دلیل ماهیت قابل‌فهم و ساده PID می‌توان آن را در عمده پردازشگرها و میکروپروسسورها قرار داد، در این میان PLC، PID Digital Controller (کنترل‌گر منطقی برنامه‌پذیر) و DCS (سیستم کنترل توزیع‌شده) از اهمیت ویژه‌تری برخوردار هستند.

در مورد PLC و DCS پیش‌تر مفصل صحبت کرده‌ایم. اگر بخواهیم یک مثال برای استفاده از PID در PLC داشته باشیم می‌توانیم به موضوع کنترل فشار با استفاده از پی‌ال‌سی نگاهی داشته باشیم.

در شکل زیر یک پی‌ال‌سی را با دو ماژول آنالوگ ورودی و خروجی مشاهده می‌کنید، ماژول ورودی این PLC به Pressure sensor and transmitter متصل شده است و به‌صورت لحظه‌ای مقدار فشار را اندازه‌گیری می‌کند.

از سوی دیگر این PLC با استفاده از ماژول خروجی آنالوگ خود می‌تواند به Variable flow valve (شیر متغیر جریان) فرمان باز شدن یا بسته شدن را بدهد.

باتوجه‌به این توضیحات، بخش اول در حکم فیدبک برای PID و بخش دوم برای کنترل می‌باشد. ادامه کار که به محاسبات PID و مقایسه مقدار خطا (انحراف از میزان فشار مدنظر) و میزان Set-point مربوط می‌گردد در بخش CPU واقع در PLC صورت می‌پذیرد.

به زبان ساده‌تر ما در CPU پی‌ال‌سی، PID خود را تعریف می‌کنیم و پس از آن سایر موارد به‌صورت خودکار تحلیل و پردازش خواهند شد.

اما PID Digital Controller چیست؟

یک سری تجهیزات هستند که معمولاً فقط توانایی کنترل PID را دارا هستند و امکان اجرای سایر برنامه‌ها در آنها وجود ندارد. البته این تجهیزات در انواع مختلفی ساخته می‌شوند که توانایی کنترل یک تا چند لوپ کنترلی را به‌صورت هم‌زمان دارا هستند.

کاربرد PID

باتوجه‌به اینکه PID برای ما کنترل حول یک نقطه (SetPoint) را ارائه می‌کند می‌تواند کاربردهای فراوانی داشته باشد و در عمل نیز به همین صورت است و به همین دلیل شاهد کنترل‌کننده‌های اختصاصی PID در بازار نیز هستیم.

کاربردهای PID در رنج وسیعی از موارد مانند؛ عملیات حرارتی فلزات، خشک‌کردن، تبخیر کردن حلال‌ها، مسائل فرادمایی، پخت فرم‌های متفاوتی از عناصر و … استفاده می‌شود.

طراحی MPPT (ردیابی نقطه حداکثر توان)

اگر خاطرتان باشد در دوره سیمولینک متلب پروژه‌ای در مورد MPPT و چگونگی حداکثر کردن توان سلول‌های خورشیدی انجام دادیم، ازآنجایی‌که مشخصه جریان – ولتاژ یک سلول فتوولتائیک به دما و سطح تابش بستگی دارد؛ بنابراین جریان و ولتاژ، به نسبت تغییر شرایط جوی، تغییر خواهد کرد؛ بنابراین ردیابی نقطه توان حداکثر برای یک سیستم فتوولتائیک کارا بسیار مهم است. برای پیداکردن MPPT، کنترل‌کننده PID مورداستفاده قرار می‌گیرد و برای آن جریان و ولتاژ نقطه موردنظر به کنترل‌کننده داده می‌شود. اگر شرایط جوی تغییر کند این دنبال‌کننده، ولتاژ و جریان را ثابت نگه می‌دارد.

همان‌طور که مشاهده کردید PID کاربردهای زیادی دارد ولی بااین‌حال مهم‌ترین کاربرد PID همچنان در بحث مسائل دمایی می‌باشد که در ادامه به شکل خاص‌تری به آن می‌پردازیم.

کنترلر دمای PID

دو روش اصلی برای تنظیم کنترلر دما با استفاده از مقادیر PID وجود دارد.

۱. یک مهندس برق متغیرهای P، I، D، و توان موردنیاز فرآیند جهت تنظیم دما را به‌صورت دستی به دست آورد.

۲. با وارد نمودن مقادیر هدف و استفاده از ساختار خود – تنظیمی کنترلر دما، PID خودش ضرایب را محاسبه و مستقیماً کنترل نماید.

در هر دو روش، PID مقدار توان موردنیاز جهت تثبیت دمایی را به ما می‌دهد که حالا می‌تواند به‌صورت دستی یا خودکار باشد.

انتخاب کنترل‌کننده دما PID

حلقه تنظیم PID در انواع کنترلرهای دمایی به تعداد مختلف استفاده می‌شود. متداول‌ترین حالت کنترلر دما، انجام محاسبات PID و مدیریت تک فرآیندی است.

تجهیزات پزشکی برای اطمینان از ثابت ماندن دما برای استریلیزه شدن کامل ابزارها، از کنترلر دمای PID تک حلقه استفاده می‌کنند. حس‌گر دما در داخل مخزن استرلیزاسیون دما را اندازه گرفته و به کنترلر می‌دهد تا توان سیستم گرمادهی را افزایش یا کاهش دهد.

برنامه چند حلقه کنترلر دمای PID پیچیدگی بیشتری دارد، در این برنامه کنترلر چندین فرآیند را هم‌زمان پردازش می‌کند. بااین‌حال هر فرآیند مستقل بوده و حلقه منحصربه‌فرد خودش را دارد و اختلال در یک فرآیند روی سایرین تأثیری ندارد. برای مثال یک نانوایی ممکن است چند اجاق فر داشته باشد که همگی دمایی یکسان داشته باشند اما هیچ‌کدام روی دیگری تأثیری نمی‌گذارند و درنهایت تمام این مجموعه توسط یک کنترلر دمای PID چند حلقه کنترل شود.

کنترل‌های PID با حلقه‌های کنترلی آبشاری

برخی کنترلرهای PID قابلیت‌های بهبودیافته‌ای دارند و می‌توانند حلقه‌های مرتبط را بجای حلقه‌های مستقل اجرا کنند.

در کنترل آبشاری، دو حلقه مرتبط باهم به‌صورت اولیه و ثانویه عمل می‌کنند. حلقه اولیه عنصر اصلی فرآیند تحت گرما را کنترل می‌کند درحالی‌که روی قسمت گرما دهنده کنترلی ندارد. حلقه ثانویه اما در عوض همانند ژاکتی به دور حلقه اول قرار گرفته و توسط گرما دهنده تاثیر می‌پذیرد. کنترلر PID دمای هر دو حلقه را اندازه‌گیری می‌کند و توان اعمالی مؤثر بر گرمای قسمت ثانویه را تنظیم کرده تا درنهایت گرمای بخش اولیه را به حد تنظیمی برساند.

میزان‌سازی یا تنظیم کردن (Tuning) برای حلقه آبشاری امری ضروری است چرا که برخلاف سایر متدها ممکن است با اورشوت‌های (Overshoot) ناخواسته‌ای مواجه شود. در این روش کنترلر PID با رسیدن دما به حد تنظیمی (Setpoint) توان را کاهش می‌دهد تا دما در همان مقدار ثابت بماند. یک مثال مناسب برای این روش آب‌کردن شکلات است، شکلات اگر خودش مستقیماً در معرض حرارت قرار گیرد می‌سوزد اما در کاسه‌ای که روی آب جوش قرار دارد به‌راحتی ذوب می‌شود. شکلات حلقه اولیه است، ماده‌ای حساس که درنهایت باید حرارت ببیند، و کاسه آب که نقش واسطه‌ای بین تجهیز گرما دهنده و حلقه اولیه را دارد، حلقه ثانویه است. حلقه‌های آبشاری، قواعد عملکردی یکسانی دارند اما از جهت بزرگی مقیاس و دقت کنترل دما می‌توانند نسبت به یکدیگر متفاوت ظاهر شوند.

کنترل دمای PID چند ناحیه‌ای

کنترلرهای دمای PID چند ناحیه‌ای برای مدیریت فرآیندهایی‌اند که در چند ناحیه جریان دارند، فرآیند کنترلی یکی است اما عنصر تحت حرارت به‌قدری بزرگ است که ممکن است بین نواحی مختلف آن اختلاف دما وجود داشته باشد.

برای مثال در اجاق فر صنعتی با ۶ قسمت گرما دهنده مختلف، دما در کل اجاق باید یکسان باشد اما ممکن است برخی از نقاط باعث ایجاد تفاوت دمایی شوند. چون فرآیند به دمایی یکپارچه در تمام نواحی نیاز دارد. راه‌حل؛ استفاده از کنترلر دمای PID چند ناحیه‌ای برای کنترل هر ۶ قسمت گرما دهنده است، بنابراین ۶ حلقه کنترلی وجود خواهد داشت که به‌صورت هم‌زمان در حال اجرا هستند. کنترلر PID هرکدام از این ۶ قسمت را به‌صورت جدا کنترل می‌کند تا دما در تمامی نواحی اجاق فر روی حد تنظیمی ثابت بماند. ^[6]

توسعه PID

یکی از مسائلی که اخیراً موردتوجه بیشتری واقع شده است، مبحث PID فازی می‌باشد.

هم‌اکنون با پیشرفت الگوریتم‌های هوشمند، ضرورت استفاده از PID فازی به‌عنوان بهینه‌ترین کنترلر برای ما بیش‌ازپیش آشکار شده است.^[7] تکنولوژی کنترل فازی PID برای کنترل دمای کوره در مقایسه با نوع کلاسیک و حتی PI فازی آن به دلیل سادگی، انعطاف‌پذیر بودن، پایداری و دقت، کاربرد بهتری دارد و برای رهایی از بند محدودیت‌هایی که در عمل برای کنترل دما به‌صورت زمان واقعی پیش می‌آیند، استفاده از کنترلر PID فازی پیشنهاد می‌شود.^[8]

پس اگر در بحث مقاله‌نویسی به دنبال موضوعی خاص و البته به‌روز می‌باشید می‌توانید نگاهی به بحث PID فازی داشته باشید.

سؤالات متداول PID

سخن پایانی

PID حقیقتاً یکی از کارآمدترین ابزارها جهت کنترل فرآیندهای SetPoint محور می‌باشد که توانسته به‌خوبی خود را در بازار به اثبات برساند به همین دلیل داشتن دانش تخصصی در این زمینه قطعاً می‌تواند برای شما مفید و کاربردی بوده و سبب استفاده بهتر از فرصت‌های پیشرو گردد. چیزی که مشخص است قطعاً PID در این سطح نخواهد ماند و پیشرفت‌های بیشتری را به خود خواهد دید به همین دلیل توصیه می‌کنم در سازوکار و طراحی آن بیشتر عمیق شوید.

منابع

1. Khan Nouman, Zaman Asim, Khan Qasim, “Comprehensive Study on Performance of PID Controller and its Applications“, Electronic and Automation Control Conference (IMCEC), DOI: 10.1109/IMCEC.2018.8469267, May 2018 ↑

2. Hills, Richard L, “Power From the Wind”, Cambridge University Press, 1996 ↑

3. N. Minorsky, “Directional Stability of Automatically Steered Bodies“, Journal of the American Society for Naval Engineers, May 1922 ↑

4. پیمان پربها، “کنترل PID به زبان آدمیزاد!”، ویرایش اول ↑

5. Aidan O’Dwyer, “Handbook of PI and PID controller tuning rules”, Imperial College Press, June 2009 ↑

6. “What is a PID Temperature Controller?“, West Control Solutions. ↑

7. D. Shilane, J. S. Martikainen and S. Dudoit, “A general frame-work for statistical performance comparison of evolutionary computation algorithms“, Information Sciences, Journal, Vol:178, pp. 2870-2879 , july 2008 ↑

8. D. B. Fogel, “Evolutionary Computation: Toward a New Philosophy of Machine Intelligence“, Wiley-IEEE Press, 2006 ↑

خوشحال خواهیم شد اگر شما نکته و یا تجربه‌ای در مورد PID داشته‌اید با ما در بخش نظرات در میان بگذارید.

راستی! برای دريافت مطالب جديد در پیج اینستاگرم PowreEn عضو شويد.