روش های بهینه سازی در مهندسی برق

آموزش‌ها
آپدیت شده در : 21/ 08/ 1402
نویسنده : مهندس سیاه تیری
۱ دیدگاه

روش‌های بهینه سازی در مهندسی برق

اگر به پایان نامه‌های مقاطع کارشناسی ارشد و دکتری نگاهی بیاندازید متوجه خواهید شد که کلمه “بهینه سازی” شاه کلید اکثر پایان نامه‌ها می‌باشد. البته این داستان صرفا به دانشگاه محدود نمی شود و در صنعت نیز بیش از آنکه شاهد ابداعات جدید باشیم در راستای پاسخ به نیازها، بهینه سازی‌های گوناگونی صورت می‌پذیرد.

باتوجه به اهمیت بهینه سازی (Optimization) در برق و سایر رشته‌های مهندسی، روش‌های گوناگونی که ترکیبی از علوم متفاوت و بخصوص ریاضیات می‌باشند به وجود آمده اند، این روش‌ها هرکدام مزیت و معایب خاص خود را داشته و درنهایت این شما هستید که با توجه به نیازتان گزینه مناسب را انتخاب خواهید نمود.

هدف از بهینه‌سازی یافتن بهترین مقدار از میان گروهی از مقادیر ممکن است، به طوریکه این مقدار بهینه، محدودیت‌هایی را تامین نماید.

آنچه که در این نوشتار خواهید خواند؛

کمی قبل‌تر از بهینه سازی
بهینه سازی چیست
روش های اساسی بهینه سازی
روش‌های شمارشی
روش‌های محاسباتی (جستجوی ریاضی)
روش‌های ابتكاری و فرا ابتکاری (جستجوی تصادفی)
انواع روش‌های منتخب بهینه‌سازی
مفاهیم اساسی در بهینه سازی
الگوریتم‌های بهینه‌سازی قطعی و احتمالی
الگوریتم بهینه‌سازی هیوریستیک و متاهیوریستیک
الگوریتم بهینه‌سازی با روش جستجوی اتفاقی
الگوریتم هوک و جیوز
روش پاول
الگوریتم ژنتیک
سردسازی (تبرید) شبیه سازی شده
الگوریتم بهینه‌سازی انبوه ذرات
مقایسه و انتخاب روش بهینه‌سازی مناسب
الگوریتم ژنتیک
بهینه‌سازی در الگوریتم ژنتیک
مزایای الگوریتم ژنتیک
معایب الگوریتم ژنتیک
انتخاب شما و دلیل آن

کمی قبل‌تر از بهینه سازی

بهینه سازی باید بروی یک سری داده‌ها صورت بپذیرد، پس قطعا قبل از آن مرحله دیگری نیز وجود دارد، به عنوان مثال اگر هدف ما بهینه سازی یک ماشین الکتریکی باشد؛ باید در ابتدا تمام معادلات و معلومات این ماشین الکتریکی نظیر؛ توان، ولتاژ، سرعت، بارگذاری مغناطیسی، ضریب سیم پیچی، نسبت قوس به گام قطب، تعداد شیار هرفاز به ازای هر قطب، ضریب انباشتگی شیار و … مشخص شده باشند. به زبان ساده ابتدا بروی کاغذ ماشین الکتریکی ما آماده شده باشد و سپس با درنظر گرفتن گذاره ای مانند؛ حداکثر سازی توان، حداقل سازی تلفات، کاهش حجم ماشین، افزایش چگالی گشتاور و … (یک و یا چند مورد) اقدام به بهینه سازی آن نماییم.

بهینه سازی چیست

هینه‌سازی در ریاضیات، اقتصاد و مدیریت به برگزیدن بهترین عضو از یک مجموعه از اعضای دست یافتنی اشاره می شود. در ساده‌ترین شکل تلاش می‌شود که با گزینش نظام مند داده‌ها از یک مجموعه قابل دستیابی و قابل محاسبه، بیشینه و کمینه یک تابع حقیقی به دست آید.[1]

بهینه‌سازی یك فعالیت مهم و تعیین‌كننده در طراحی ساختاری است. طراحان زمانی قادر خواهند بود طرح‌های بهتری تولید كنند كه بتوانند با روش‌های بهینه‌سازی در صرف زمان و هزینه طراحی صرفه‌جویی نمایند. بسیاری از مسائل بهینه‌سازی در مهندسی برق، طبیعتاً پیچیده‌تر و مشكل‌تر از آن هستند كه با روش‌های مرسوم بهینه‌سازی نظیر روش برنامه‌ریزی ریاضی و نظایر آن قابل حل باشند.

بهینه‌سازی تركیبی (Combinational Optimization) و جستجو برای یافتن نقطه بهینه توابع با متغیرهای گسسته (Discrete Variables) دو روش جدید برای پاسخ به نیازهای امروز مهندسی می‌باشند.

امروزه بسیاری از مسائل بهینه‌سازی تركیبی كه اغلب از جمله مسائل با درجه غیر چندجمله‌ای (NP-Hard) هستند، به صورت تقریبی با كامپیوترهای موجود قابل حل می‌باشند. از جمله راه‌حل‌های موجود در برخورد با این گونه مسائل، استفاده از الگوریتم‌های تقریبی یا ابتكاری است.

این الگوریتم‌ها تضمینی نمی‌دهند كه جواب به دست آمده بهینه باشد و تنها با صرف زمان بسیار می‌توان جواب نسبتاً دقیقی به دست آورد و در حقیقت بسته به زمان صرف شده، دقت جواب تغییر می‌كند.

تمرکز ما در این پست بروی روش‌های ابتکار و فراابتکاری می‌باشد.

روش‌های اساسی بهینه سازی

سیستم‌های کامپیوتری در دهه‌های گذشته به شکل چشمگیری پیشرفت کرده اند به همین دلیل در طول زمان نیز شاهد روش‌های جدید بهینه سازی بوده ایم که اغلب آنها با استفاده از کامپیوتر مورد استفاده قرار می‌گیرند، در تصویر شماره 1-1 تمام روش‌های اساسی بهینه سازی به همراه زیرشاخه‌های آنها آورده شده است که در ادامه به بررسی سرشاخه‌های آنها می‌پردازیم؛

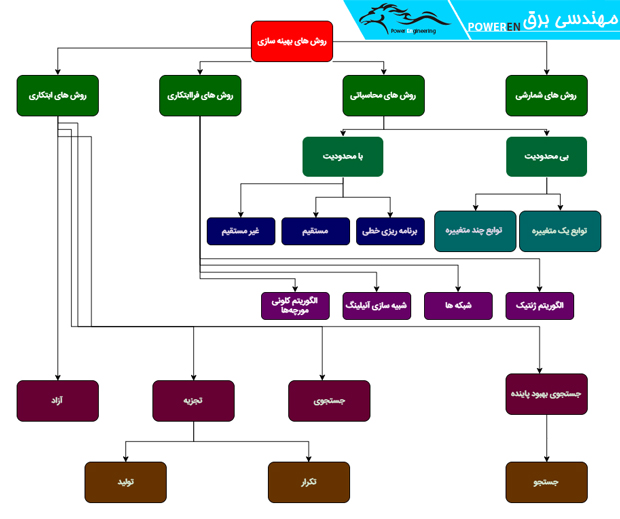
تمام روش های بهینه سازی

روش‌های شمارشی

در روش‌های شمارشی (Enumerative Method)، در هر تكرار فقط یك نقطه متعلق به فضای دامنه تابع هدف، بررسی می‌شود. این روش‌ها برای پیاده‌سازی، ساده‌تر از روش‌های دیگر می‌باشند؛ اما به محاسبات قابل توجهی نیاز دارند. در این روش‌ها سازوکاری برای كاستن دامنه جستجو وجود ندارد و دامنه فضای جستجو شده با این روش خیلی بزرگ می‌باشد. برنامه‌ریزی پویا (Dynamic Programming) مثال خوبی از روش‌های شمارشی می‌باشد. این روش كاملاً غیرهوشمند بوده و به همین دلیل امروزه بندرت به تنهایی مورد استفاده قرار می‌گیرد.

روش‌های محاسباتی (جستجوی ریاضی)

روش جستجوی ریاضی (Based Method Calculus) از مجموعه شرایط لازم و كافی كه در جواب مسأله بهینه‌سازی صدق می‌كند، استفاده می‌كند. وجود یا عدم وجود محدودیت‌های بهینه‌سازی در این روش نقش اساسی دارند. به همین علت، این روش به دو دسته با محدودیت و بدون محدودیت تقسیم می‌گردد.

روش محاسباتی بدون محدودیت

روش‌های بهینه‌سازی بدون محدودیت با توجه به تعداد متغیرها شامل بهینه‌سازی توابع یك متغیره و چند متغیره می‌باشند.

روش‌های بهینه‌سازی توابع یك متغیره، به سه دسته روش‌های مرتبه صفر، مرتبه اول و مرتبه دوم تقسیم می‌شوند. روش‌های مرتبه صفر فقط به محاسبه تابع هدف در نقاط مختلف نیاز دارد؛ اما روش‌های مرتبه اول از تابع هدف و مشتق آن و روش‌های مرتبه دوم از تابع هدف و مشتق اول و دوم آن استفاده می‌كنند. در بهینه‌سازی توابع چند متغیره كه كاربرد بسیار زیادی در مسائل مهندسی دارند، كمینه‌سازی یا بیشینه‌سازی یك كمیت با مقدار زیادی متغیر طراحی صورت می‌گیرد.

روش محاسباتی با محدودیت

یك تقسیم‌بندی، روش‌های بهینه‌سازی با محدودیت را به سه دسته؛ برنامه‌ریزی خطی، روش‌های مستقیم و غیرمستقیم تقسیم می‌كند. مسائل با محدودیت كه توابع هدف و محدودیت‌های آنها خطی باشند، جزء مسائل برنامه‌ریزی خطی قرار می‌گیرند. برنامه‌ریزی خطی شاخه‌ای از برنامه‌ریزی ریاضی است و كاربردهای فیزیكی، صنعتی و تجاری بسیاری دارد.

در روش‌های مستقیم، نقطه بهینه به طور مستقیم جستجو شده و از روش‌های بهینه‌یابی بدون محدودیت استفاده نمی‌شود. هدف اصلی روش‌های غیرمستقیم استفاده از الگوریتم‌های بهینه‌سازی بدون محدودیت برای حل عمومی مسائل بهینه‌سازی با محدودیت می‌باشد.

در اكثر روش‌های محاسباتی بهینه‌یابی، از گرادیان تابع هدف برای هدایت جستجو، استفاده می‌شود. اگر مثلاً به علت ناپیوستگی تابع هدف، مشتق آن قابل محاسبه نباشد، این روش‌ها اغلب با مشكل روبه‌رو می‌شوند.

روش‌های ابتكاری و فرا ابتکاری (جستجوی تصادفی)

یك روش ناشیانه برای حل مسائل بهینه‌سازی تركیبی این است كه تمامی جواب‌های امكان‌پذیر در نظر گرفته شوند و توابع هدف مربوط به آنها محاسبه شوند و در نهایت، بهترین جواب انتخاب گردد. روشن است كه شیوه شمارش كامل، نهایتاً به جواب دقیق مسأله منتهی می‌شود؛ اما در عمل به دلیل زیاد بودن تعداد جواب‌های امكان‌پذیر، استفاده از آن غیرممكن است. با توجه به مشكلات مربوط به روش شمارش كامل، همواره بر ایجاد روش‌های مؤثرتر و كاراتر تأكید شده است. در این زمینه، الگوریتم‌های مختلفی به وجود آمده است كه مشهورترین نمونه آنها، روش سیمپلكس برای حل برنامه‌های خطی و روش شاخه و كرانه برای حل برنامه‌های خطی با متغیرهای صحیح است. برای مسائلی با ابعاد بزرگ، روش سیمپلكس از كارایی بسیار خوبی برخوردار است، ولی روش شاخه و كرانه كارایی خود را از دست می‌دهد و عملكرد بهتری از شمارش كامل نخواهد داشت. به دلایل فوق، اخیراً تمركز بیشتری بر روش‌های ابتكاری (Heuristic)، فرا ابتکاری (Metaheuristic) یا جستجوی تصادفی (Random Method) صورت گرفته است.

روش‌های جستجوی ابتكاری عمدتاً بر مبنای روش‌های شمارشی می‌باشند، با این تفاوت كه از اطلاعات اضافی برای هدایت جستجو استفاده می‌كنند. این روش‌ها از نظر حوزه كاربرد، كاملاً عمومی هستند و می‌توانند مسائل خیلی پیچیده را حل كنند. عمده این روش‌ها، تصادفی بوده و از طبیعت الهام گرفته شده‌اند.

روش‌های جستجوی ابتكاری، روش‌هایی هستند كه می‌توانند جوابی خوب (نزدیك به بهینه) در زمانی محدود برای یك مسأله ارائه كنند.

باتوجه به اینکه هدف ما صرفا بررسی بهینه سازی تحت رشته مهندسی برق می‌باشد در ادامه منتخب ترین روش‌های بهینه سازی که در اکثر موارد توسط محققین این رشته مورد استفاده قرار می‌گیرند بررسی خواهند شد.

پس از مقایسه این روش ها، یکی از آنها به عنوان روش مناسب‌تر انتخاب شده و در پایان به بررسی دقیق‌تر آن خواهیم پرداخت. دقت داشته باشید که این پست صرفا برای اهداف بهینه سازی در رشته مهندسی برق نگارش شده و از این پس نیز تصور می‌کنیم که هدف ما بهینه سازی یک موتور الکتریکی می‌باشد.

انواع روش‌های منتخب بهینه‌سازی

با توجه به فراوانی تعداد پارامترهای درگیر در طراحی ماشین‌های الکتریکی و نیز معادلات غیرخطی که ارتباط بین پارامترها را پیچیده‌تر می‌کند، طراحی ماشین‌های الکتریکی یک مساله‌ی غیرخطی چند بعدی است که با محاسبات دستی نمی توان به نتایج بهینه دست یافت. لذا طراحی بهینه‌ی ماشین‌های الکتریکی نیازمند روش‌های تحلیل و محاسبه‌ی کامیپوتری می‌باشد که بتوان الگوریتم عملکرد آنها را طراحی و به کامپیوتر تعریف کرد.

مفاهیم اساسی در بهینه سازی

پیش از پرداختن به انواع روش‌های بهینه‌سازی متداول در طراحی ماشین‌های الکتریکی، لازم است مفاهیم زیر تعریف شوند:

تابع هدف (Objective function)

یک تابع ریاضی است که مقصود نهایی از اجرای بهینه‌سازی یافتن مقدار بهینه برای آن می‌باشد. این مقدار بهینه معمولا مقدار اکسترمم (ماکزیمم یا مینیمم) تابع هدف است که باید محدودیت‌هایی (معادله و نامعادله محدودیت) را نیز رعایت کرده باشد. در رابطه‌ی زیر، هدف یافتن مقدار بهینه‌ی z بوده، F تابع هدف و تابعی از متغیرهای X_1،X₂… و X_n می‌باشد.

(1-1) $C:\Users\M.E\Desktop\10_files\image001.png$ $C:\Users\M.E\Desktop\10_files\image002.png$

پارامترهای بهینه‌سازی (Optimization parameters)

در تعریف فوق از تابع هدف، X_1،X₂… و X_n در رابطه‌ی (1-1) پارامترهای بهینه‌سازی محسوب می‌شوند. به عبارتی پارامترهای بهینه‌سازی متغیرهایی هستند که مقدار بهینه‌ی تابع هدف با توجه به وابستگی‌اش به آن متغیرها به دست می‌آیند.

فضای مساله یا فضای جست‌وجو (Problem space or search space)

تمامی مجموعه مقادیری که امکان دارد مقدار بهینه را به دست بدهند. هر یک از مجموعه مقادیر X مجاز، در رابطه‌ی (1-1) یک نقطه در فضای مساله‌ی n بعدی و به عبارتی کاندیدای جواب (Solution candidate) است.

بهینه‌سازی محلی (Local optimization) و بهینه‌سازی سراسری (Global optimization)

در مسائل بهینه‌سازی محلی، هدف یافتن مقدار ماکزیمم یا مینیمم تابع هدف نسبت به مقادیر همسایگی در فضای مساله است در حالی که در بهینه‌سازی کلی، مقصود به دست آوردن مقدار ماکزیمم یا مینیممی است که به ازای کلیه‌ی مقادیر فضای مساله به دست آمده باشد. در طراحی ماشین‌های الکتریکی به دنبال یافتن مقدار بهینه‌ی سراسری هستیم.

شایستگی یا برازندگی (Fitness)

ارجحیت یا میزان بهینه بودن یک کاندیدای جواب توسط شایستگی آن تعیین می‌شود. در واقع تابع هدف توسط تابع شایستگی به برنامه کامپیوتری معرفی می‌شود و مقدار مایکزیمم و مینمم بودن تابع شایستگی است که تابع هدف را بهینه می‌کند. به عنوان یک مثال ساده اگر در یک مساله‌ی بهینه‌سازی یک بعدی، تابع شایستگی f(x)=3x-4 بوده و هدف یافتن مقدار حداکثر باشد، با توجه به کمتر بودن f(x₁=1)=-1 از f(x₂=2)=2، x₂کاندیدای شایسته تری نسبت به x₁ است.

نامعادله و معادله‌ی محدودیت (Constraint inequalities and equalities)

به صورت کلی در مسائل غیرخطی، مقادیر مشخصی از پارامترهای بهینه‌سازی X_1،X₂… و X_n را باید طوری محاسبه کرد که نامعادله‌ی محدودیت (2-1) همراه با معادله‌ی محدودیت (3-1) برقرار باشند. می‌توان محدودیت‌ را بازده‌ی قابل قبولی برای پارامترهای بهینه‌سازی تعریف کرد.

(1-2) $C:\Users\M.E\Desktop\10_files\image003.png$ $C:\Users\M.E\Desktop\10_files\image004.png$

(1-3) $C:\Users\M.E\Desktop\10_files\image005.png$ $C:\Users\M.E\Desktop\10_files\image006.png$

رابطه‌ی خاصی بین تعداد متغیرها (n) و تعداد محدودیت‌های k وجود ندارد. بنابراین در هر مساله k می‌تواند بزرگتر، کوچکتر و یا مساوی با n باشد. به مسائلی که در آنها k برابر با صفر است، بهینه‌سازی بدون محدودیت اطلاق می‌شود.

الگوریتم‌های بهینه‌سازی قطعی و احتمالی

عموما الگوریتم‌های بهینه‌سازی سراسری را می‌توان در دو دسته‌ی قطعی و احتمالی بررسی کرد.

الگوریتم‌های قطعی دسته‌ای هستند که رابطه‌ی معناداری بین کاندیدای احتمالی جواب و شایستگی آن وجود داشته باشد. اگر ارتباط بین کاندیدای جواب و شایستگی آن واضح نباشد یا خیلی پیچیده باشد، معرفی جواب بهینه به طور قطعی ممکن نبوده و ناچار از الگوریتم‌های احتمالی استفاده خواهد شد. در الگوریتم‌های قطعی حداکثر یک راه برای ادامه‌ی الگوریتم وجود دارد که با نفی شدن آن، الگوریتم به پایان رسیده و مقدار بهینه‌ی سراسری معرفی می‌شود. در واقع هیچ یک از مراحل الگوریتم‌های قطعی از اعداد یا روابط تصادفی استفاده نمی کند و ارتباط بین مراحل کاملا مشخص و به طور ریاضی قابل تعریف است. به دست آوردن مقدار اکسترمم با استفاده از مشتق گیری از ساده‌ترین نمونه‌های الگوریتم قطعی است. الگوریتم‌های احتمالی ممکن است مقدار بهینه‌ی محلی را معرفی کنند اما این به معنای نادرست بودن نتیجه آنها نیست. در واقع از الگوریتم‌های احتمالی در شرایطی استفاده می‌شود که الگوریتم قطعی برای حل مساله یا وجود ندارد یا بسیار زمان‌بر است. در این شرایط یافتن یک مقدار بهینه‌ی محلی قطعا بهتر از نرسیدن به هیچ جوابی است.

در برخی مواقع حل مسئله با استفاده از الگوریتم قطعی می‌تواند 10¹⁰⁰ سال به‌طول بیانجامد!.

الگوریتم‌های بهینه‌سازی مستقیم و غیر مستقیم

تحلیل مسائل غیر خطی می‌تواند به روش مستقیم یا غیر مستقیم انجام شود. در روش مستقیم، محدودیت‌ها به صورت مستقیم به الگوریتم حل اعمال می‌گردند ولی در روش‌های غیر مستقیم، ابتدا محدودیت‌ها را به بهینه‌سازی بدون محدودیت تبدیل و سپس به حل آن اقدام می‌شود.[2]

انواع روش‌های مستقیم و غیر مستقیم عبارتند از:

روش‌های مستقیم:

روش‌های جستجوی هیوریستیک (Heuristic)
روش‌های با محدودیت تقریبی
روش‌های جهت ممکن

روش‌های غیر مستقیم:

روش حذف محدودیت ها
روش تابع جریمه داخلی
روش تابع جریمه خارجی

الگوریتم بهینه‌سازی هیوریستیک و متاهیوریستیک (Metaheuristic)

هیوریستیک در واقع بخشی از الگوریتم بهینه‌سازی است که در تصمیم گیری راجع به مرحله‌ی بعدی الگوریتم نقش اصلی را ایفا می‌کند. به این معنی که کاندیدهای جواب یک مرحله را مقایسه کرده و تصمیم می‌گیرد از کدام یک در شکل دهی کاندیداهای جواب در مرحله بعد استفاده شود. الگوریتم متاهیوریستیک روش حلی برای مسائل بهینه‌سازی عمومی است که توابع هیوریستیک و توابع هدف را ترکیب کرده و با آنها مثل یک جعبه‌ی سیاه عمل می‌کند.

الگوریتم بهینه‌سازی با روش جستجوی اتفاقی (Stochastic algorithm)

این روش بر مبنای دستیابی به مقدار حداقل تابع با تقریب کمتری از مقدار قبلی و تکرار این عمل استوار است. الگوریتم جستجوی اتفاقی را می‌توان در مراحل زیر خلاصه کرد:

گام 1: انتخاب نقطه‌ی شروع X و طول گام ƛ_i برای n متغیر (i=1,2, … ,n)

گام 2: ایجاد عدد تصادفی U_i

گام 3: تدوین بردار S_i= U_iƛ_i

گام 4: محاسبه‌ی F(X+S)

گام 5: اگر F(X+S)<F(X) باشد، افزایش X در جهت S ادامه می‌یابد و تا وقتی که بهبود حاصله در تابع هدف ناچیز شود، این روند را ادامه داده و به گام 2 بر می‌گردد.

گام 6: اگر F(X+S)>F(X) باشد مقدار F(X-S) محاسبه شود.

گام 7: اگر F(X-S)<F(X) باشد، افزایش X در جهت -S ادامه می‌یابد و تا وقتی که بهبود حاصله در تابع هدف ناچیز شود، این روند را ادامه داده و به گام 2 بر می‌گردد.

گام 8: اگر بهبودی در تابع هدف در هیچ یک از جهت‌ها حاصل نشود، جهت S ناموفق خوانده می‌شود. الگوریتم به گام 2 برمی گردد.

گام 9: با استفاده از یک ضریب کاهش از طول گام کاسته شده و به گام 2 رجوع می‌شود.

گام 10: وقتی طول گام از دقت مورد نیاز کمتر شود، تکرار محاسبات متوقف خواهد شد.

این روش زمان زیادی برای همگرایی نیاز دارد و کاملا وابسته به نقطه‌ی شروع است.

الگوریتم هوک و جیوز (Hook and Jeeves method)

در این روش از شیوه‌ی جستجوی شکل کلی استفاده می‌شود. یعنی در هرگام دو عمل انجام می‌شود یکی عملکرد موضعی تابع هدف و دیگری استفاده از شکل کلی. الگوریتم زیر این روش را به طور گام به گام تشریح می‌کند؛

گام 1: مقدار اولیه X را انتخاب و مقدار F(X) را محاسبه کنید.

گام 2: با جستجوی موضعی در هر جهت و افزایش دیفرانسیلی هر متغیر به میزان Δx_iو محاسبه‌ی تابع هدف درهر مرحله، امکان دستیابی به تابع هدف با کمترین مقدار بررسی می‌شود.

گام 3: چنانچه بهبود در تابع هدف حاصل نشود، از اندازه‌ی دیفرانسیل کاسته و جستجو از بهترین نقطه‌ی قبلی ادامه می‌یابد.

گام 4: در صورت کاهش مقدار تابع هدف، با استفاده از نقاط مراحل قبل ( $C:\Users\M.E\Desktop\10_files\image008.png$ ) مقدار نقطه‌ی موقت ( $C:\Users\M.E\Desktop\10_files\image009.png$ ) از رابطه $C:\Users\M.E\Desktop\10_files\image010.png$ محاسبه می‌شود.

گام 5: اگر نقطه‌ی موقت به کاهش مقدار تابع هدف منجر شود، جستجوی موضعی جدید انجام شده و در نقطه‌ی جدید مقدار تابع هدف محاسبه می‌شود.

گام 6: اگر نقطه‌ی موقت به کاهش مقدار تابع هدف منجر شود، جستجوی موضعی جدید انجام شده و در نقطه‌ی جدید مقدار تابع هدف محاسبه می‌شود.

گام 7: چنانچه تفاوت بین مقادیر تابع هدف در گام آخر و ماقبل آن کمتر از مقدار مشخص شده به عنوان خطا باشد، عملیات خاتمه می‌یابد.

این روش از روش جستجوی اتفاقی کندتر است ولی از دقت بیشتری برخوردار است.

روش پاول (Powell method)

این روش تعمیم روش قبل بوده و از ویژگی همگرایی درجه دوم برخوردار است. از آنجاییکه می‌توان بیشتر توابع را در نزدیکی مقدار حداقل آنها با دقت بالا توسط توابع درجه‌ی دوم تقریب زد، روش پاول از بازدهی بالایی برخوردار است. الگوریتم این روش به صورت زیر می‌باشد.[3]

گام 1: با انتخاب بردار شروع X₀(0)، جهت‌های جستجوی M_i(0) موازی با محورهای اصلی انتخاب می‌شوند.

گام 2: برای بهینه‌سازی تابع در n جهت اولیه با استفاده از تقریب درجه دوم، توالی جستجوی یک متغیره ایجاد می‌شود.

گام 3: با جابجایی متغیرها به صورت $C:\Users\M.E\Desktop\10_files\image011.png$ متغیر جدید ایجاد می‌شود. در این حالت $C:\Users\M.E\Desktop\10_files\image012.png$ آخرین نقطه از توالی جستجوی یک متغیره و $C:\Users\M.E\Desktop\10_files\image013.png$ نقطه‌ای است که در بین دو جستجوی متوالی منجر به بیشترین بهبودی در مقدار تابع می‌شود.

گام 4: اگر در مقدار تابع هدف در $C:\Users\M.E\Desktop\10_files\image012.png$ بهبودی نسبت به نقطه شروع $C:\Users\M.E\Desktop\10_files\image014.png$ حاصل نشده باشد، آخرین نقطه یعنی $C:\Users\M.E\Desktop\10_files\image012.png$ به عنوان نقطه‌ی شروع جدید انتخاب شده و گروه جستجوی یک متغیره در جهت‌های قبلی انجام می‌شود.

گام 5: وقتی همگرایی حاصل می‌شود که تفاضل مقادیر توابع در تکرارهای متوالی از مقدار مشخص شده به عنوان خطا کمتر باشد.

الگوریتم ژنتیک (Genetic Algorithm)

الگوریتم ژنتیک به عنوان یک ابزار بهینه‌سازی قدرتمند در مسائل مختلف بهینه‌سازی مورد استفاده قرار می‌گیرد. در این الگوریتم ابتدا ورودیها و محدوده‌ی تغییرات آنها مشخص می‌شود. هریک از ورودی‌ها به عنوان ژن در الگوریتم ژنتیک عمل می‌کنند. ژن‌ها در کنار هم تشکلی کروموزوم را داده و چندین کروموزوم در کنار هم یک جمعیت را تشکیل می‌دهند. مقدار تابع هدف برای هر کروموزوم با توجه به مقادیر اختصاص یافته به ژن‌های آن کروموزوم قابل محاسبه است. در واقع کروموزوم‌های تشکیل دهنده‌ی جمعیت همان کاندیدهای جواب هستند.

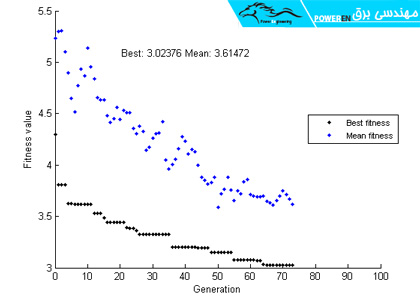
الگوریتم ژنتیک در متلب

اولین قدم در الگوریتم ژنتیک ایجاد جمعیت اولیه به صورت تصادفی است. در ادامه جمعیت هر نسل با توجه به نسل قبل تولید می‌شود. به منظور تولید نسل بعد (بازتولید – Reproduction) عملیات انتخاب – Selection، تزویج یا تقاطع – Cross over و جهش – Mutation بر روی کروموزوم‌ها انجام می‌شود. روند پیش روی الگوریتم و بازتولید طوری است که جمعیت جدید را با هدف تولید نسل بهتر (تابع هدف بهینه تر) و حذف کروموزوم‌های ضعیف تولید نماید.

سردسازی (تبرید) شبیه سازی شده (Simulated Annealing)

سردسازی شبیه سازی شده از روند فیزیکی سرچشمه می‌گیرد که در آن ابتدا یک جامد را داغ کرده و سپس به تدریج سرد می‌کنند. گرما باعث پخش اتم‌ها در فضای جامد می‌شود. به تدریج با سرد شدن جامد، اتم‌ها ساختاری را به خود می‌گیرند که دارای حداقل انرژی باشد (مینمم سراسری). این روش کاربرد بسیاری در الگوریتم‌های مربوط به یافتن مینیمم محلی دارد. مشکل این روش ناکارآمد بودن آن در فضای جستجوی وسیع است. معمولا سردسازی شبیه سازی شده در ترکیب با سایر روش‌های بهینه‌سازی ابزار قدرتمندی است.^[4]

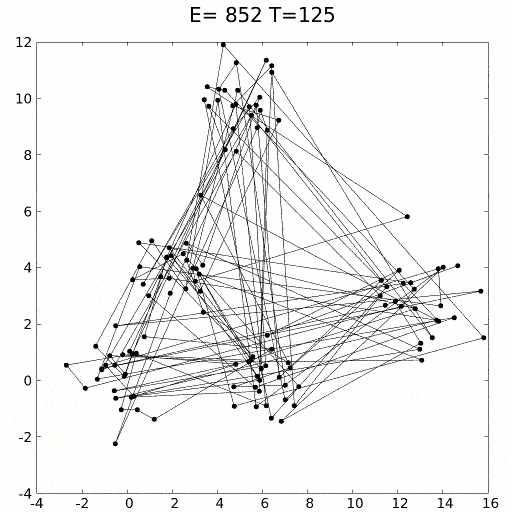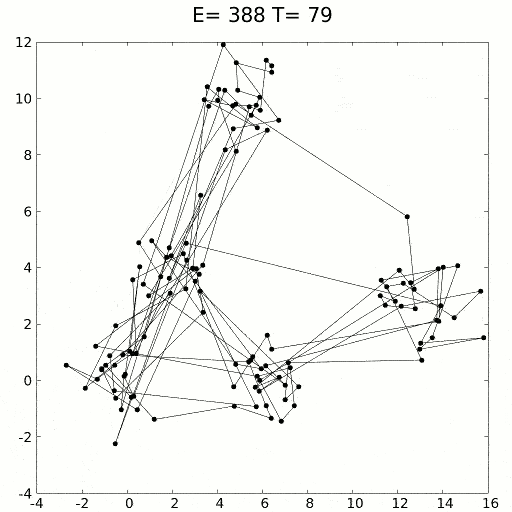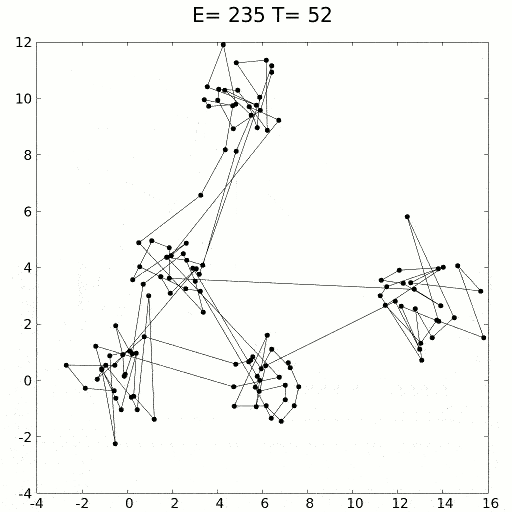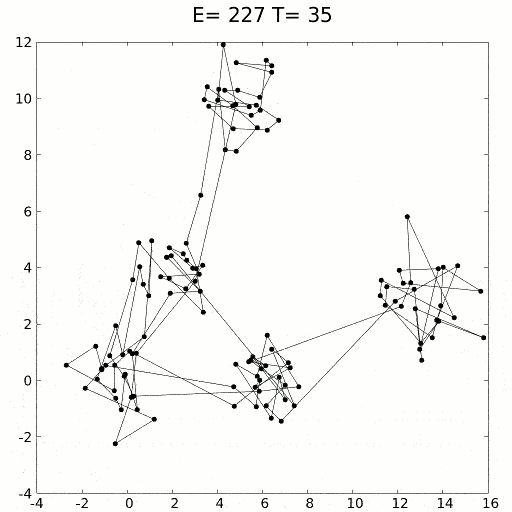
بهینه سازی به روش سردسازی

الگوریتم بهینه‌سازی انبوه ذرات (PSO)

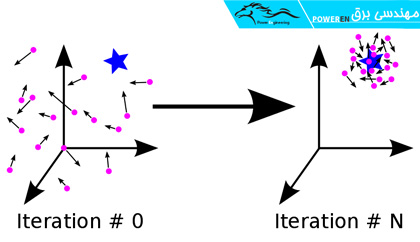
تکنیک PSO

Particle Swarm Optimization برگرفته از حرکت گروهی انبوهی از زنبورها (ذرات) است که سعی در یافتن محلی با بیشترین تعداد گل را دارند. در واقع می‌توان PSO را تعمیم یافته‌ی روش جستجوی اتفاقی دانست. مسیر جستجوی محل بهینه با استفاده از دانش هر زنبور و زنبورهای مجاور آن ادامه می‌یابد.^[5]

هز ذره در الگوریتم PSO از سه بردار n بعدی تشکیل شده است که n، بعد فضای جستجو می‌باشد. برای ذره‌ی iام این سه بردار عبارتند از: $C:\Users\M.E\Desktop\10_files\image015.png$ موقعیت فعلی ذره، $C:\Users\M.E\Desktop\10_files\image016.png$ سرعت فعلی حرکت ذره و $C:\Users\M.E\Desktop\10_files\image017.png$ بهترین موقعیتی که ذره تا به حال تجربه کرده است. در هر مرحله‌ای که الگوریتم تکرار می‌شود، $C:\Users\M.E\Desktop\10_files\image015.png$ به عنوان یک کاندیدای جواب محاسبه می‌شود. اگر این موقعیت بهتر از جواب‌های پیشین باشد در $C:\Users\M.E\Desktop\10_files\image017.png$ ذخیره می‌شود. این روند تا جایی ادامه می‌یابد که بهترین جواب حاصله از دو مرحله‌ی متوالی اخیر دارای اختلاف کمی باشند. الگوریتم پایان یافته و جواب آخرین مرحله به عنوان مقدار بهینه معرفی می‌شود.^[6]

مقایسه و انتخاب روش بهینه‌سازی مناسب

ازمیان روش‌های بهینه‌سازی استفاده شده در علوم مختلف، روش‌های تکاملی (Evolutionary algorithms) بیشتر در طراحی ماشین‌های الکتریکی محبوبیت یافته‌اند. الگوریتم‌های تکاملی در هر مرحله تعدادی از کاندیداهای جواب را شامل می‌شوند که اساس تولید جواب‌های مرحله بعد خواهند بود. ارتباط بین دو مرحله‌ی متوالی معمولا از یکی از روش‌های الهام گرفته از طبیعت بهره می‌گیرد. همچون روش الگوریتم ژنتیک که از تولید نسل جدید (فرزندان) توسط جمعیت ماقبل (والدین) استفاده می‌کند و روش انبوه ذرات یا گروه مورچگان (Ant Colony) که همگی از رفتار ذاتی و طبیعی حیوانات و حشرات برای یافتن بهترین وضعیت موجود در محیط اطراف بهره گرفته‌اند.

معیارهایی که در مسائل طراحی و بهینه‌سازی ماشین‌های الکتریکی به منظور انتخاب مناسب‌ترین روش بهینه‌سازی وجود دارد عبارتند از:

زمان لازم برای همگرایی محاسبات و الگوریتم حداقل باشد.
نتایج دقیق‌تری حاصل شود.
مراحل و محاسبات الگوریتم کمترین میزان مشتق‌های مرتبه اول و دوم را شامل شود.
در مراحل تکرار در حل مسائل، کمترین میزان تخلف از محدودیت‌ها رخ دهد.
نقطه‌ی اکسترمم به دست آمده نتیجه‌ی بررسی کل فضای مساله باشد، به عبارتی اکسترمم سراسری باشد نه محلی.

از بین روش‌های متداول، الگوریتم ژنتیک دارای زمان تحلیل مناسب‌تر، دقت محاسبات قابل قبول و عاری از مشتقات مرتبه اول و دوم می‌باشد. در ادامه مزایا و معایب الگوریتم ژنتیک در مقایسه با سایر روش‌های بهینه‌سازی ذکر می‌شود.^[7]

در دهه هفتاد میلادی دانشمندی از دانشگاه میشیگان به نام جان هلند ایده استفاده از الگوریتم ژنتیک را در بهینه‌سازی‌های مهندسی مطرح کرد. ایده اساسی این الگوریتم انتقال خصوصیات موروثی توسط ژن‌هاست.

مزایای الگوریتم ژنتیک در مقایسه با سایر روش‌های بهینه‌سازی

1). اولین و مهمترین نقطه‌ی قوت الگوریتم ژنتیک موازی بودن آن است. به این معنی که در الگوریتم ژنتیک جمعیتی از نقاط به صورت موازی و هم زمان به جای یک نقطه مورد جستجو قرار می‌گیرند. روش‌های پرکاربرد دیگر همچون بهینه‌سازی انبوه ذرات موازی نبوده و یک نقطه یا مسیر پیش روی تصادفی انتخاب می‌شود. در صورت بهتر نبودن این مسیر از مسیر قبلی، کل کارهای انجام شده بیهوده بوده و به کناری گذاشته می‌شود و الگوریتم از گام‌های اول دوباره شروع می‌شود. از آنجایی که GA چند نقطه‌ی شروع دارد، در یک لحظه می‌تواند فضای مساله را از چند جهت مختلف جستجو کند و در صورت به نتیجه نرسیدن سایر راه‌ها ادامه می‌یابد. گرچه الگوریتم ژنتیک عموما روش بهینه‌سازی سریعی محسوب نمی شود ولی موازی بودن روند پیش روی آن سبب می‌شود که نسبت به سایر روش‌های تکاملی و احتمالی سریع‌تر باشد.^[8]

2). با توجه به موازی بودن الگوریتم ژنتیک، این روش برای مسائلی که فضای مساله‌ی چند بعدی و

وسیعی دارند بسیار مناسب است.

3). الگوریتم ژنتیک چیزی از طبیعتِ مساله‌ای که حل می‌کند نمی داند. این موضوع باعث می‌شود که تمام فضای سه بعدی را بدون ارجحیت قائل شدن برای بخشی از فضاء، جستجو کند.

4). در GA نیاز به اطلاع از مشتقات تابع هدف نیست و کافی است بتوان یک تابع برازش (Fitness function) برای آن تعریف کرد به گونه‌ای که میزان شایستگی تابع هدف را مشخص کند. لذا بر خلاف روش‌های بهینه‌سازی قطعی که نیاز به مشتقات تابع هدف دارند، الگوریتم ژنتیک یک روش بهینه‌سازی احتمالی است.

5). با افزایش دادن ضریب جهش می‌توان پراکندگی ژنها را در مراحل بعدی افزایش داد. این مساله

موجب پوشش دادن کل فضای جستجو شده و لذا GA در مسائل با فضای جستجو نویزی مفید و کارآمد است.

6). یکی دیگر از مزایای الگوریتم ژنتیک این است که به راحتی می‌توان از آن برای مسائل تک هدفه (Single objective) و نیز چند هدفه (Multi objective) استفاده کرد. در مسائل چند هدفه، قصد یافتن مقدار بهینه را برای چند پارامتر (تابع هدف) به طور همزمان داریم.

7). روش‌های متعددی برای سرعت دهی به الگوریتم و بهبود کیفیت جواب وجود دارد که به محض

افزایش آگاهی از دامنه‌ی مساله از این روش‌ها می‌توان استفاده کرد و رفته‌رفته سرعت پیش روی الگوریتم را افزایش داد.

معایب الگوریتم ژنتیک در مقایسه با سایر روش‌های بهینه‌سازی

با اینکه الگوریتم ژنتیک یکی از گزینه‌های مناسب برای بهینه سازی می‌باشد با این حال معایبی نیز دارد که در ادامه به آنها خواهیم پرداخت؛

چگونگی نوشتن تابع هدف

یکی از مشکلات الگورتیم ژنتیک چگونگی نوشتن تابع هدف است. تابع هدف در جعبه ابزار بهینه‌سازی GA در نرم افزار MATLAB توسط تابع شایستگی که همان تابع برازش است به کامپیوتر معرفی می‌شود. سراسری یا محلی بودن کروموزوم بهینه‌ی معرفی شده وابستگی شدیدی به تابع شایستگی، اندازه‌ی جمعیت، نرخ جهش و تقاطع دارد. البته با چند مرتبه اجرای برنامه به صورت سعی و خطا می‌توان در مورد مناسب بودن تابع برازش معرفی شده اطمینان حاصل کرد.

نارس بودن جواب

مشکل دیگر که آن را نارس بودن جواب (Premature) می‌نامند این است که اگر یک کروموزوم فاصله‌اش با سایر کروموزوم‌های نسل‌اش زیاد بوده و در نسل‌های نخستین نیز ایجاد شده باشد، محدودیت ایجاد کرده و پیش از آنکه کل فضای جستجو بررسی شود، جواب نهایی اعلام خواهد شد. این اتفاق معمولا در جمعیت‌های کم اتفاق می‌افتاد. در این مورد هم می‌توان با سعی و خطا و اجرای چندباره‌ی بهینه‌سازی تعداد جمعیت مناسب برای مساله را انتخاب کرد.

با توجه به نکات ذکر شده، با انتخاب مناسب چگونگی تعریف تابع هدف، تعداد جمعیت و نرخ جهش و تقاطع، روش بهینه‌سازی الگوریتم ژنتیک (GA) به عنوان یک روش مناسب برای ماشین‌های الکتریکی انتخاب می‌گردد.

Genetic algorithm تکنیک جستجو در علم رایانه برای یافتن راه‌حل تقریبی برای بهینه‌سازی مدل، ریاضی و مسائل جستجو است. الگوریتم ژنتیک نوع خاصی از الگوریتم‌های تکاملی است که از تکنیک‌های زیست‌شناسی فرگشتی مانند وراثت، جهش زیست‌شناسی و اصول انتخابی داروین برای یافتن فرمول بهینه جهت پیش‌بینی یا تطبیق الگو استفاده می‌شود.^[9]

الگوریتم ژنتیک

در سال 1859 میلادی، داروین (Charles Darwin) کتاب معروف خود را تحت عنوان “منشا انواع” (On the Origin of species) منتشر کرد. در این کتاب داروین نظریه‌ی انتخاب طبیعی و بقای اصلح را که در میان تمام انواع جانداران و گیاهان جاری است برای اولین بار مطرح کرد. نظریه‌ی فوق در واقع نیروی طبیعت در بهینه‌سازی انواع گونه‌ها طی یک تکامل بیولوژیکی را مطرح می‌کند.

برداشت داروین از قاعده‌ی تولید مثل فرزندان یک گونه توسط والدین، یک الگوریتم منظم را تبیین می‌کرد که بعدها پایه و اساس بسیاری از شاخه‌های علوم مختلف گردید. تاجاییکه در مسائل مهندسی با کاربرد در روش‌های بهینه‌سازی تحت عنوان الگوریتم ژنتیک وارد شد و سپس نقطه‌ی شروع و اساس بسیاری از روش‌های بهینه‌سازی دیگر شد. پیش از پرداختن به جزییات مراحل بهینه‌سازی طراحی ماشین توسط این الگوریتم لازم است اصطلاحات ذیل تعریف گردند:

ژن: ژن‌ها (Gene) پارامترهای تاثیرگذار بر تابع هدف هستند.

کروموزوم: هر گروه از ژن‌ها که تابع هدف به ازای آنها محاسبه می‌شود یک کروموزوم (Chromosome) یا DNA را تشکیل می‌دهد. طول یک کروموزوم برابر با تعداد پارامترهای تاثیرگذار بر تابع هدف است و بعد فضای جستجو را تعیین می‌کند. لذا وقتی راجع به فضای مساله یا فضای جستجوی n بعدی صحبت می‌شود منظور این است که هر کروموزوم شامل n ژن بوده و به عبارتی طول کروموزوم‌ها n است.

نسل: کروموزوم‌ها در هر مرحله از الگوریتم ژنتیک، نسل (Generation) مربوط به آن مرحله را تشکیل می‌دهند.

جمعیت: تعداد کورموزوم‌های هر نسل، جمعیت (Population) نامیده می‌شود.

فرزندان: نسل جدید تولید شده از نسل قبل (والدین) را فرزندان (Children or offspring) می‌نامیم.

والدین: نسل تولیدکننده‌ی نسل بعد (فرزندان)، والدین (Parents) هستند.

مساله‌ی بهینه‌سازی طراحی را می‌توان در یک فضای n بعدی تعریف کرد که n برابر با تعداد پارامترهای بهینه‌سازی است. جواب یک مساله‌ی بهینه‌سازی در نهایت توسط مجموعه‌ای از پارامترهای بهینه‌سازی به شکل X = {x₁,x₂, … ,x_n} تعریف می‌شود. در الگوریتم ژنتیک (GA) هر پارامتر بهینه‌سازی (x₁ و x₂ و …) یک ژن و هر مجموعه‌ی X متشکل از ژنهای یک کروموزوم نامیده می‌شود. در روش GA جستجو در فضای مساله توسط یک روش تکاملی انجام می‌گیرد.^[10] ابتدا جمعیت اولیه به طور تصادفی تشکیل می‌شود. هر کروزموزوم متناظر با یک نقطه در فضای مساله است. مقدار تابع هدف برای هر کروموزوم محاسبه می‌شود. به عنوان مثال اگر حصول مقدار ماکزیمم تابع هدف مطلوب باشد، کزوموزوم‌های ضعیف که مقدار تابع هدف محاسبه شده برای آنها کمتر از بقیه است حذف شده و کروموزوم‌های باقی مانده در نقش والدین، بازتولید نسل آینده یا فرزندان را برعهده می‌گیرند. بازتولید نسل جدید توسط یکی از سه روش انتخاب، تقاطع و جهش انجام می‌گیرد که در ادامه هر روش توضیح داده خواهد شد. پس از تولید نسل جدید، دوباره مقدار تابع هدف برای هر کروموزوم محاسبه شده و روند بازتولید فرزندان توسط والدین ادامه می‌یابد^[11]. این حلقه تا وقتی تکرار می‌شود که تابع هدف حاصله از کروموزوم‌های آخرین نسل به مقدار مطلوب برسد. ضوابط این مقدار مطلوب را معمولا توسط تعداد نسل‌ها یا اختلاف بین بهترین مقدار حاصله از دو نسل اخیر متوالی تعیین می‌نمایند.^[12] گام‌های طی شده در الگوریتم ژنتیک را می‌توان به طور خلاصه به‌ترتیب زیر بیان کرد:

تولید تصادفی کرموموزوم‌های اولین نسل
محاسبه‌ی تابع هدف برای کروموزوم‌ها و انتخاب بهترین مقادیر
اتمام الگوریتم در صورت حصول ضوابط تعیین شده برای اتمام
بازتولید نسل جدید از نسل قبل و بازگشت به مرحله دوم

بازتولید نسل جدید توسط یکی از سه روش انتخاب، تقاطع و جهش انجام می‌گیرد. در ادامه هر یک از این روش‌ها توضیح داده می‌شود.

انتخاب (selection)

معمولا پس از انتخاب تعداد کروموزوم‌های برتر هر نسل، تعدادی از بهترین‌ها عینا در نسل بعدی تکرار می‌شوند. این روش بازتولید را “انتخاب” می‌نامند. تعداد کروموزوم‌های برتر انتخاب شده معمولا کمتر از 2 درصد جمعیت نسل بعد را تشکیل می‌دهد.

تقاطع (cross over)

اپراتور تقاطع به گونه‌ای عمل می‌کند که 2 کروموزوم به عنوان والدین دریافت کرده و حداکثر 2 فرزند ایجاد می‌کند. هریک از فرزندان خصوصیاتی را از هریک از والدینش به ارث می‌برد. در واقع کروموزوم مربوط به فرزند، بعضی از ژنها را از یکی از والدین و باقی را از والد دیگرش دریافت می‌کند. اپراتور تقاطع می‌تواند تک نقطه‌ای (SPX – Single Point Crossover)، دو نقطه‌ای (TPX – Tow Point Crossover)، و یا چند نقطه‌ای (MPX – Multi Point Crossover) باشد. شکل 1-2 هر یک از انواع اپراتورهای تقاطع را برای کروموزوم‌هایی با 10 ژن به تصویر می‌کشد.

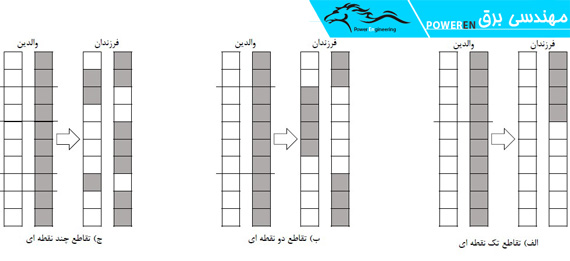
شکل 1-2: بازتولید نسل جدید با استفاده از تقاطع

جهش (mutation)

اپراتور جهش یک روش بازتولید نسل جدید مهم به منظور حفظ تنوع کروموزوم‌ها می‌باشد. در این روش ژن‌های تشکیل دهنده‌ی کروموزوم‌های فرزندان از تغییرات جزئی و تصادفی در ژن‌های کروموزوم‌های والدین به دست می‌آید. این تغییرات تصادفی طوری انجام می‌شود که هر ژن در محدوده‌ی مجاز خود باقی بماند.

معمولا بیش از 60% کروموزوم‌های نسل جدید از روش تقاطع و باقی کروموزوم‌ها از اعمال جهش در نسل قبل به وجود می‌آیند.

بهینه‌سازی در الگوریتم ژنتیک

در استفاده از روش بهینه‌سازی الگوریتم ژنتیک، دو گام اساسی و اولیه مورد توجه ویژه هستند: انتخاب توابع هدف و انتخاب پارامترهای بهینه‌سازی متناظر با آنها. در ادامه به شرح دقیق تابع هدف و پارامترهای دخیل در بهینه‌سازی خواهیم پرداخت.

تابع هدف بهینه‌سازی

با توجه به پروژه ای که قرار است شما آن را بهینه‌تر نمایید، تابع هدف نیز مشخص می‌شود، به عنوان مثال در یک ماشین الکتریکی تابع هدف می‌تواند؛ بازده ماشین، کاهش تلفات آن، کاهش حجم ماشین و … باشد، البته در برخی موارد ممکن است تابع هدف واحد نبوده و بیش از یک مورد باشد.

در بیشتر شبیه سازی‌های ماشینی، تابع هدف؛ افزایش بازده خروجی می‌باشد چرا که در این حالت متغیرهای بیشتری دست‌خوش تغییرات می‌گردند.

پارامترهای بهینه‌سازی

پارامترهای بهینه‌سازی باید به گونه‌ای انتخاب شوند که اولا بیشترین تاثیر را بر توابع هدف گذاشته و ثانیا ارتباطی با یکدیگر نداشته باشند و یا ارتباطشان با یکدیگر در نظر گرفته شود به طوریکه اختلالی در حصول نتیجه مطلوب به وجود نیاورند. ویژگی سوم انتخاب مناسب پارامترهای بهینه‌سازی تعریف بازه‌ی قابل قبول برای آنهاست به طوری که این بازه به اندازه‌ی کافی وسیع باشد تا فضای جستجو بی دلیل محدود نگردد و نیز به طور منطقی محدود شده باشد و مقادیر غیرقابل قبول آن پارامتر را شامل نشود.

با توجه به اهمیت پارامترها به همین دلیل سعی می‌شود در ابتدا یک گذاره کلی در نظر بگیریم و سپس برای رسیدن به آن گذاره، ضرایبی که امکان بهینه شدن در راستای آن گذاره را دارند، انتخاب نماییم.

هر یک از پارامترهای بهینه‌سازی به عنوان یک ژن شناخته شده و یک مجموعه کامل از آنها، کروموزوم را تشکیل می‌دهند.

انتخاب شما و دلیل آن

در این پست سعی کردیم به صورت مختصر اما کاملا علمی به روش‌های مطرح بهینه سازی بخصوص برای رشته مهندسی برق بپردازیم، قطعا این روش‌ها دارای جزئیات بسیاری می‌باشند که سبب شده برای هر روش شاهد کتاب‌های متنوعی باشیم، اگر به یکی از روش‌های ذکر شده نیاز پیدا کردید قطعا منابع خوبی در دسترس شما خواهد بود.

در پایان با توجه به بررسی‌های صورت گرفته روش الگوریتم ژنتیک انتخاب ما بود اما قطعا کسانی هستند که از روش‌های دیگری، جهت بهینه سازی استفاده نموده اند، اگر شما نیز جزء کسانی هستید که روشی به غیر از ژنتیک را انتخاب کرده اید خوشحال خواهیم شد اگر دلایلتان را در قسمت نظرات برای ما قرار دهید.

منابع

[1] Piryonesi, Sayed Madeh; Tavakolan, Mehdi (9 January 2017). “A mathematical programming model for solving cost-safety optimization (CSO) problems in the maintenance of structures”. KSCE Journal of Civil Engineering, 2018

[2] S. Rao Singiresu, “Engineering Optimization: Theory and Practice”, 3rd Edition, Wiley, 1996

[3] Rong-jie Wang, M.J. Kamper, K. Van der Westhuizen, J.F. Gieras, “Optima design of a coreless stator axial flux permanent-magnet generator.”, IEEE Transactions on Magnetics, Vol.41 no.1 pp.55-64, 2005.

[4] A. Duan, D.M. lonel, “A review of recent developments in electrical machine design optimization methods with a permanent magnet synchronous motor benchmark study”, IEEE Energy Conversion Congress and Exposition (ECCE), 2011.

[5] J. Robinson, Y. Rahmat-Samii, “Particle swarm optimization in electromagnetics”, IEEE Transactions on Antennas and Propagation, vol.52 no.2 pp.397-407, 2004.

[6] D. Rodger, P.C. Coles, N. Allen, H.C. Lai, P.J. Leonard and P. Roberts, “3D finite element model of a disc induction machine”, Conference Publication no.444, IEE, 1997.

[7] Yong-Hwan Oh, Tae-Kyung Chung, Min-Kyu Kim, Hyun-Kyo Jung, “Optimal design of electric machine using genetic algorirthms coupled with direct method”, IEEE Transactions on Magnetics, Vol.35 no.3 pp.1742-1745, 1999.

[8] J.J Yin, W.K.S. Tang and K.F. Man, “A comparison of optimization algorithms for biological neural network identification”, IEEE Transactions on Electron, Vol.57 no.3 pp.1127-1131, 2010.

[9] نظام‌الدین فقیه، توازن خط تولید با الگوریتم ژنتیک

[10] G.F Uler, O.A. Mohammad, Chang-seop Koh, “Design optimization of electrical machines using genetic algorithms”, IEEE Transactions on Magnetics, Vol.31 no.3 pp.2008-2011, 1995.

[11] Yong-Hwan Oh, Tae-Kyung Chung, Min-Kyu Lim, Hyun-Kyo Jung, “Optimal design of electric machine using generic algorithms coupled with direct method”, IEEE Transactions on Magnetics, vol.35 no.3 pp.1742-1745, May, 1999.

[12] R.Wrobel, P.H. Mellor, “Design consideration of a direct drive brushless PM machine with concentrated windings”, IEEE International Conference On Electric Machines and Drives, May, 2005.

اطلاع رسانی با ایمیل

1 دیدگاه

جدیدترین

قدیمی‌ترین محبوب‌ترین

Inline Feedbacks

View all comments

Mahdi

2 سال پیش

سلام
در آخر که بازده به عنوان تابع هدف انتخاب شده است در جعبه ابزار متلب به چه صورت وارد میشود؟؟؟ آیا باید رابطه ای برا آن در قسمت ادیتور متلب با پسوند m فایل ذخیره کرد یا روش دیگری باید انجام داد، ممنون میشم راهنمایی کنید.

گرایش رشته تحصیلی

قدرت

پاسخ