پخش بار نیوتون رافسون در متلب
-
آپدیت شده در :

با توجه به پیشرفت نرم افزارها، پخش بار یک سیستم چند باسه را می توان با نرم افزارهای متعددی نظیر: دیگسایلنت، ای تپ، متلب و … انجام داد و در تمام آنها نیز شاهد دقت بسیار بالا هستیم.
با توجه به اهمیت پخش بار، امروز برآن شدیم تا برای شما عزیزان یک پروژه پخش بار را جهت استفاده قرار دهیم.
در ابتدا اجازه دهید انواع روش های گرفتن پخش بار را به صورت تئوری برایتان مرور نماییم؛
روش های محاسبه پخش بار
- روش گوس سایدل
- روش نیوتن رافسون
- روش Decoupled
- روش Fast Decoupled
- روش پخش بار DC
روش گوس سایدل
گاوس سایدل (Gauss–Seidel method) در جبر خطی عددی، روش تکراری است که برای حل دستگاه معادلات خطی استفاده میشود. نام این روش از روی ریاضیدانان آلمانی کارل فریدریش گاوس و فیلیپ لودویگ ون سایدل نهاده شده است. اگرچه از این روش میتوان در هر ماتریسی که دارای درایه قطری صفر نباشد استفاده کرد، اما فقط در صورتی همگرایی تضمین میشود که ماتریس مثبت معین یا قطری غالب باشد.
برای یک سیستم مربعی باn معادلهٔ خطی و دارای مجهولx داریم:
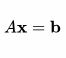
که در آن:
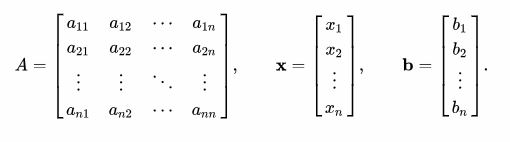
اگر A را به ماتریس پایین مثلثی و بالا مثلثی L* و U تجزیه کنیم:

معادلات خطی سیستم به شکل زیر بازنویسی خواهند شد:
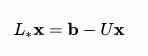
روش گاوس سایدل از روش تکراری برای حل قسمت چپ عبارت، جهت به دست آوردن x بهره میبرد، و بدین منظور از مقدار قبلی x در سمت راست عبارت استفاده میکند. میتوان آن را به صورت زیر نوشت:
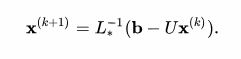
و با استفاده از خواص ماتریس مثلثی L* میتوان x(k+1) را به صورت زیر به دست آورد:
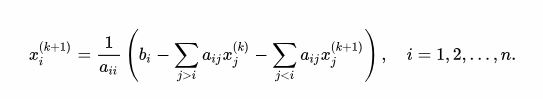
در واقع برای محاسبه (xi(k+1 به همه عناصر (x(k به جز خود آن به (xi(k دیگر نیاز خواهد شد.
محاسبات تا زمانی ادامه داده میشود تا در تکراری خاص به خطایی کمتر از مقدار مورد نظر برسیم.
روش نیوتن رافسون
این روش نیز یکی از راه های تعین ریشهٔ یک تابع است (روش مورد استفاده در این پروژه).
![]()
فرض کنید تابعی (نمودار آبی) دارید که میخواهید ریشه (محل برخورد تابع با محور xها) را بیابید یا به اصطلاح آن را حل کنید. در روش نیوتن رافسون ابتدا x0 را به عنوان حدس اولیه وارد فرمول زیر میکنیم تا x1 بدست آید. به همین ترتیب ادامه میدهیم و این بار x1 را در فرمول قرار میدهیم.
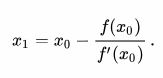
به همین ترتیب خواهیم داشت:
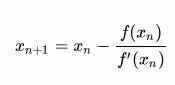
هر چه تعداد دفعات تکرار بیشتر باشد x بدست آمده به ریشه نزدیکتر است.
روش Decoupled
تجربه نشان می دهد که تغییرات P و δ بسیار زیاد بهم وابسته اند. همچنین Q و |V| نیز بهم وابسته اند پس می توان عناصر N و J ماتریس ژاکوبین را برابر صفر قرار داد.به این روش جداسازی یا Decoupled گفته می شود. معادلات توان اکتیو و راکتیو بصورت زیر در می آید:
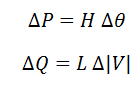
در این روش سرعت محاسبات بطور قابل ملاحظه ای افزایش می یابد اما دقت محاسبات کاهش می یابد.
روش Fast Decoupled
می توان روش Decoupled را برای تسریع در همگرایی باز تقریب زد و با قراردادن اختلاف زاویه بین شین ها برابر صفر معادلات را ساده تر کرد که به این روش Fast Decoupled می گویند. معادلات در این روش بصورت زیر در می آید:
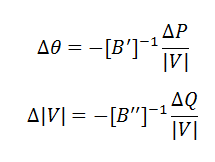
روش پخش بار DC
در این روش مقدار تقریبی توان خطوط محاسبه می شود. در این روش از مقاومت خطوط صرف نظر کرده و ولتاژ شین ها را برابر 1puو اختلاف زاویه بین شین ها را کوچک در نظر می گیریم. معادله توان در این روش بصورت زیر در می آید:
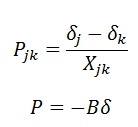
در ابتدا اجازه بدهید چند استاندارد رسمی برای حل سیستم های چند باسه را توضیح دهیم؛
شین در محاسبات
شین های استفاده شده در محاسبات و سیستم معمولاً به سه نوع دسته بندی می شوند:
شین مرجع (Slack)
این شین که به شین نیروگاهی معروف است به عنوان شین مرجع یا (Slack) در نظر گرفته می شود. زاویه در این شین، صفر درجه و ولتاژ معمولا یک پریونیت در نظر گرفته می شود. پس از محاسبات پخش بار، کمبود تولید و تلفات سیستم توسط این شین باید جبران شود. این شین را معمولا شین شماره 1 در نظر می گیریم و در این شین مقادیر |V| و δ معلوم و مقادیر P و Q مجهول می باشد.
شین های کنترل شده
شین های دارای ژنراتور هستند و به شین های کنترل شده یا PV معروف اند، زیرا در این نوع از شین ها ولتاژ و توان اکتیو مقداری معلوم دارد. در انجام محاسبات، ما باید به دنبال پیدا کردن مقدار فاز و توان راکتیو این شین ها می باشیم.
شین های بار
در این نوع شین ها توان اکتیو و راکتیو مشخص است و ولتاژ و فاز قسمت مجهول است که باید محاسبه شود. این شین ها به شین های PQ نیز موسوم هستند.
معمولاً باس شماره یک باس مرجع و باس های 1 تا m باس های کنترل ولتاژ و باس های m+1 تا n باس های مصرفی شماره گذاری می شوند.
در یک سیستم قدرت برای تحلیل، پارامترهای مهمی از هر باس باید در نظر گرفته بشوند که عبارتند از؛
- اندازه ولتاژ |V|
- زاویه فاز δ
- توان اکتیو P
- توان راکتیو Q
اجازه بدهید به سراغ فایل شبیه سازی برویم:
در این پروژه ما به روش نیوتن – رافسون به تحلیل یک شبکه 33 باسه مشخص می پردازیم و در نهایت توان های اکتیو، راکتیو، ولتاژ، توان، زاویه ولتاژ و … را برای هر باس بدست می آوریم.
توضیحات روش استفاده شده در متلب:
در این روش به دلیل اینکه از 3 عدد ام فایل (m-file) استفاده کرده ایم پروژه را کمی پیچیده کرده است در حالی که روش ساده تر هم وجود دارد و آن استفاده از کتابخانه پیش فرض MatPower می باشد که بدون نیاز به نوشتن یک کد خط می توانید داده های باس های خود را (3 باسه، 5 باسه و … ) تشکیل داده و با وارد کردن داده های ضروری در نهایت به راحتی فشردن یک دکمه پخش بار را تحویل بگیرید.
در ادامه به زودی روش ذکر شده را توضیح خواهیم داد.
در این پروژه شاهد 5 فایل می باشیم که در زیر برای شما کارکرد آنها را توضیح داده ایم؛
LFYBUS (مخفف لود فلو وای باس): کد تشکیل دهنده ماتریس ادمیتانس برای پخش بار
Busdata33: ماتریس اطلاعات باس برای کد LFYBUS
Linedata33: ماتریس اطلاعات خطوط برای کد LFYBUS
LFNEWTON: کد پخش بار اصلی نیوتن رافسون
BUSOUT: کد نمایش نتایج نهایی
در زیر برای شما کدهای قسمت های مختلف را قرار داده ایم که می توانید در نرم افزار متلب عینا وارد نمایید؛
LFYBUS:
load busdata33
load linedata33
j=sqrt(-1); i = sqrt(-1);
nl = linedata(:,1); nr = linedata(:,2); R = linedata(:,3);
X = linedata(:,4); Bc = j*linedata(:,5); a = linedata(:, 6);
nbr=length(linedata(:,1)); nbus = max(max(nl), max(nr));
Z = R + j*X; y= ones(nbr,1)./Z; %branch admittance
for n = 1:nbr
if a(n) <= 0
a(n) = 1;
else
end
Ybus=zeros(nbus,nbus); % initialize Ybus to zero
% formation of the off diagonal elements
for k=1:nbr;
Ybus(nl(k),nr(k))=Ybus(nl(k),nr(k))-y(k)/a(k);
Ybus(nr(k),nl(k))=Ybus(nl(k),nr(k));
end
end
% formation of the diagonal elements
for n=1:nbus
for k=1:nbr
if nl(k)==n
Ybus(n,n) = Ybus(n,n)+y(k)/(a(k)^2) + Bc(k);
elseif nr(k)==n
Ybus(n,n) = Ybus(n,n)+y(k) +Bc(k);
else
end
end
end
LFNEWTON:
clc
clear
LFYBUS
ns=0; ng=0; Vm=0; delta=0; yload=0; deltad=0;
nbus = length(busdata(:,1));
basemva=1;
accuracy=0.00001;
maxiter=100;
for k=1:nbus
n=busdata(k,1);
kb(n)=busdata(k,2); Vm(n)=busdata(k,3); delta(n)=busdata(k, 4);
Pd(n)=busdata(k,5); Qd(n)=busdata(k,6); Pg(n)=busdata(k,7); Qg(n) = busdata(k,8);
Qmin(n)=busdata(k, 9); Qmax(n)=busdata(k,10);
Qsh(n)=busdata(k, 11);
if Vm(n) <= 0 Vm(n) = 1.0; V(n) = 1 + 1i*0;
else delta(n) = pi/180*delta(n);
V(n) = Vm(n)*(cos(delta(n)) + 1i*sin(delta(n)));
P(n)=(Pg(n)-Pd(n))/basemva;
Q(n)=(Qg(n)-Qd(n)+ Qsh(n))/basemva;
S(n) = P(n) + 1i*Q(n);
end
end
for k=1:nbus
if kb(k) == 1, ns = ns+1; else
end
if kb(k) == 2 ng = ng+1; else
end
ngs(k) = ng;
nss(k) = ns;
end
Ym=abs(Ybus); t = angle(Ybus);
m=2*nbus-ng-2*ns;
maxerror = 1; converge=1;
iter = 0;
% Start of iterations
clear A DC J DX
while maxerror >= accuracy && iter <= maxiter % Test for max. power mismatch
for i=1:m
for k=1:m
A(i,k)=0; %Initializing Jacobian matrix
end
end
iter = iter+1;
for n=1:nbus
nn=n-nss(n);
lm=nbus+n-ngs(n)-nss(n)-ns;
J11=0; J22=0; J33=0; J44=0;
for i=1:nbr
if nl(i) == n || nr(i) == n
if nl(i) == n, l = nr(i); end
if nr(i) == n, l = nl(i); end
J11=J11+ Vm(n)*Vm(l)*Ym(n,l)*sin(t(n,l)- delta(n) + delta(l));
J33=J33+ Vm(n)*Vm(l)*Ym(n,l)*cos(t(n,l)- delta(n) + delta(l));
if kb(n)~=1
J22=J22+ Vm(l)*Ym(n,l)*cos(t(n,l)- delta(n) + delta(l));
J44=J44+ Vm(l)*Ym(n,l)*sin(t(n,l)- delta(n) + delta(l));
else
end
if kb(n) ~= 1 && kb(l) ~=1
lk = nbus+l-ngs(l)-nss(l)-ns;
ll = l -nss(l);
% off diagonalelements of J1
A(nn, ll) =-Vm(n)*Vm(l)*Ym(n,l)*sin(t(n,l)- delta(n) + delta(l));
if kb(l) == 0 % off diagonal elements of J2
A(nn, lk) =Vm(n)*Ym(n,l)*cos(t(n,l)- delta(n) + delta(l));end
if kb(n) == 0 % off diagonal elements of J3
A(lm, ll) =-Vm(n)*Vm(l)*Ym(n,l)*cos(t(n,l)- delta(n)+delta(l)); end
if kb(n) == 0 && kb(l) == 0 % off diagonal elements of J4
A(lm, lk) =-Vm(n)*Ym(n,l)*sin(t(n,l)- delta(n) + delta(l));end
else
end
else
end
end
Pk = Vm(n)^2*Ym(n,n)*cos(t(n,n))+J33;
Qk = -Vm(n)^2*Ym(n,n)*sin(t(n,n))-J11;
if kb(n) == 1 P(n)=Pk; Q(n) = Qk; end % Swing bus P
if kb(n) == 2 Q(n)=Qk;
if Qmax(n) ~= 0
Qgc = Q(n)*basemva + Qd(n) - Qsh(n);
if iter <= 7 % Between the 2th & 6th iterations
if iter > 2 % the Mvar of generator buses are
if Qgc < Qmin(n), % tested. If not within limits Vm(n)
Vm(n) = Vm(n) + 0.01; % is changed in steps of 0.01 pu to
elseif Qgc > Qmax(n), % bring the generator Mvar within
Vm(n) = Vm(n) - 0.01;end % the specified limits.
else, end
else,end
else,end
end
if kb(n) ~= 1
A(nn,nn) = J11; %diagonal elements of J1
DC(nn) = P(n)-Pk;
end
if kb(n) == 0
A(nn,lm) = 2*Vm(n)*Ym(n,n)*cos(t(n,n))+J22; %diagonal elements of J2
A(lm,nn)= J33; %diagonal elements of J3
A(lm,lm) =-2*Vm(n)*Ym(n,n)*sin(t(n,n))-J44; %diagonal of elements of J4
DC(lm) = Q(n)-Qk;
end
end
DX=A\DC';
for n=1:nbus
nn=n-nss(n);
lm=nbus+n-ngs(n)-nss(n)-ns;
if kb(n) ~= 1
delta(n) = delta(n)+DX(nn); end
if kb(n) == 0
Vm(n)=Vm(n)+DX(lm); end
end
maxerror=max(abs(DC));
if iter == maxiter && maxerror > accuracy
fprintf('\nWARNING: Iterative solution did not converged after ')
fprintf('%g', iter), fprintf(' iterations.\n\n')
fprintf('Press Enter to terminate the iterations and print the results \n')
converge = 0; pause, else
end
end
if converge ~= 1
tech= (' ITERATIVE SOLUTION DID NOT CONVERGE');
else
tech=(' Power Flow Solution by Newton-Raphson Method');
end
V = Vm.*cos(delta)+1i*Vm.*sin(delta);
deltad=180/pi*delta;
i=sqrt(-1);
k=0;
for n = 1:nbus
if kb(n) == 1
k=k+1;
S(n)= P(n)+1i*Q(n);
Pg(n) = P(n)*basemva + Pd(n);
Qg(n) = Q(n)*basemva + Qd(n) - Qsh(n);
Pgg(k)=Pg(n);
Qgg(k)=Qg(n); %june 97
elseif kb(n) ==2
k=k+1;
S(n)=P(n)+1i*Q(n);
Qg(n) = Q(n)*basemva + Qd(n) - Qsh(n);
Pgg(k)=Pg(n);
Qgg(k)=Qg(n); % June 1997
end
yload(n) = (Pd(n)- 1i*Qd(n)+1i*Qsh(n))/(basemva*Vm(n)^2);
end
busdata(:,3)=Vm'; busdata(:,4)=deltad';
Pgt = sum(Pg); Qgt = sum(Qg); Pdt = sum(Pd); Qdt = sum(Qd); Qsht = sum(Qsh);
BUSOUT
BUSOUT:
% This program prints the power flow solution in a tabulated form
% on the screen.
%
% Copyright (C) 1998 by H. Saadat - PowerEn.ir.
disp(tech)
fprintf(' Maximum Power Mismatch = %g \n', maxerror)
fprintf(' No. of Iterations = %g \n\n', iter)
head =[' Bus Voltage Angle ------Load------ ---Generation--- Injected'
' No. Mag. Degree MW Mvar MW Mvar Mvar '
' '];
disp(head)
for n=1:nbus
fprintf(' %5g', n), fprintf(' %7.3f', Vm(n)),
fprintf(' %8.3f', deltad(n)), fprintf(' %9.3f', Pd(n)),
fprintf(' %9.3f', Qd(n)), fprintf(' %9.3f', Pg(n)),
fprintf(' %9.3f ', Qg(n)), fprintf(' %8.3f\n', Qsh(n))
end
fprintf(' \n'), fprintf(' Total ')
fprintf(' %9.3f', Pdt), fprintf(' %9.3f', Qdt),
fprintf(' %9.3f', Pgt), fprintf(' %9.3f', Qgt), fprintf(' %9.3f\n\n', Qsht)
plot(abs(V));
در ویدیو زیر شما نحوه Run کردن این پروژه را خواهید آموخت:
توجه:
به زودی برای شما روش پخش بار استاندارد با MatPower را آموزش خواهیم داد که در آن به راحتی می توانید داده های باس های تعریف شده را تغییر نمایید.
 دانلود مستقیم فایل پخش بار نیوتون رافسون | با حجم 1 مگابایت
دانلود مستقیم فایل پخش بار نیوتون رافسون | با حجم 1 مگابایت
 دانلود مستقیم ویدیو آموزش پخش بار نیوتون رافسون در متلب – Full HD | با حجم 12 مگابایت
دانلود مستقیم ویدیو آموزش پخش بار نیوتون رافسون در متلب – Full HD | با حجم 12 مگابایت
![]() پسورد : www.poweren.ir
پسورد : www.poweren.ir
راستی! برای دریافت مطالب جدید در کانال تلگرام PowerEn عضو شوید.







سلام
ببخشید اگه بخواهیم ببینیم که یه فایل سیمولینکمون در متلب با چه روشی (گوس سایدل یا نیوتون رافسون یا …) داره پخش بار میشه از کجا باید بفهمیم؟
سلام
شما روش حل رو مشخص می کنید دیگه
بسیار سپاس گذارم
موفق باشید
سلام ببخشید من برای ۳۰باس میخوام خیلی فرق داره با ۳۳باسه؟
سلام
خیر، تفاوت آنچنانی نیست
سلام ببخشید من هم سوالم این بود فقط این سوالم داشتم ببینم اعداد هم تغییر میکنه یا نه اصلا اعداد مهمه ؟
سلام، بله قطعا اعداد مهمه
Unrecognized function or variable ‘busdata’.
هر چی اجرا میکنم این ارورو میده دقیقا نمیدونم مشکلش چیه؟
لطفا راهنمایی کنید…
سلام
نسخه متلبتون باید بالای 2017 باشه
ببخشید میتونیند در حد یک خط توضیح بدهی که a = linedata(:, 6)بیانگر چیه؟
می تونید از این آموزش استفاده کنید
آموزش سیمولینک متلب
ببخشید فایل بعد از دانلود شدن باز نمیشه
سلام باید با متلب باز بشه