کنترل فرکانس بار
-
آپدیت شده در :

هدف اصلی کنترل سیستم قدرت عبارت است از تولید توان الکتریکی در یک سیستم به هم پیوسته به صورتی که تا حد امکان قابل اطمینان و اقتصادی باشد و در عین حال ولتاژ ها و فرکانس در درون حدود مجاز قرار گرفته باشند.
قدرت اكتیو در هنگام نیاز باید تولید شود و چون مصرف بارها در ساعات مختلف شبانه روز تغییر مینمایند، لذا قدرت تولیدی ژنراتورها نیز باید كنترل گردند. قدرت خروجی یك ژنراتور با تغییر دادن قدرت مكانیكی ورودی آن كنترل میشود. برای این كار با باز كردن یا بستن شیر بخار و یا دریچه آب، جریان بخار یا آب روی توربین تنظیم شده و باعث كنترل قدرت مكانیكی و در نتیجه قدرت اكتیو خروجی ژنراتور میگردد. اگر قدرت مصرفی بار افزایش یابد، باید شیر بخار و یا دریچه آب بیشتر باز شود كه به همان میزان قدرت تولیدی ژنراتور افزایش داده شود، و چنانچه قدرت مصرفی بار كاهش یابد، باید شیر بخار و یا دریچه آب تا حدی بسته شود كه به همان میزان باعث كاهش قدرت تولیدی ژنراتور شده و در نتیجه توازن قدرت اكتیو برقرار گردد.
آنچه که در این نوشتار خواهید خواند؛
- مقدمه
- مدل سازی سیستم فرکانس بار
- كنترل بهینه درجه دو و معادله ریكاتی
- طراحی یك كنترلكننده مقاوم
- شبیه سازی در متلب
- نتیجه گیری
- منابع
عدم توازن قدرت، از تأثیر آن بر روی سرعت و یا فركانس ژنراتور حس میشود. در صورت كاهش بار و اضافه بودن تولید، ژنراتور تمایل به افزایش سرعت و فركانس خود دارد. و در صورت افزایش بار و كمبود تولید، سرعت و فركانس ژنراتور رو به كاهش میرود. انحراف فركانس از مقدار نامی آن به عنوان سیگنالی جهت تحریك سیستم كنترل خودکار انتخاب میشود. توازن قدرت اكتیو بمنزله ثابت بودن فركانس سیستم است كه این موضوع به نوبه خود دارای اهمیت فراوانی میباشد. قدرت اكتیو، زاویه قدرت δ و فركانس در یك كانال كنترل میشوند كه آن را كانال كنترل (Power Factor (PF قدرت فركانس، و یا مگاوات-فركانس مینامیم. سیستم كنترل مربوطه نیز به سیستم كنترل خودکار بار- فركانس، (Load Frequency Control (LFC معروف است.
حلقه كنترل LFC (کنترل بار-فرکانس) فقط به تغییرات كمدامنه و آرام بار و فركانس پاسخ میدهد و در شرایط اضطراری و عدم توازن قدرت ناشی از آن قادر به كنترل نمیباشد. كنترل سیستم در شرایط اضطراری و تغییرات ناگهانی با مطالعه پایداری گذرا و حفاظت سیستمها مورد بررسی قرار میگیرد.
تغییر در توان حقیقی عمدتا بر روی فرکانس سیستم تاثیر می گذارد در حالی که توان راکتیو حساسیت کمی به فرکانس دارد و بطور عمده به تغییرات اندازه ولتاژ وابسته است. بنابراین توان حقیقی و راکتیو به صورت جداگانه کنترل می شوند. حلقه، کنترل فرکانس بار LFC، توان حقیقی و فرکانس را کنترل می کند و حلقه تنظیم خود کار ولتاژ (Automatic Voltage Regulator (AVR، نیز توان راکتیو و اندازه ولتاژ را تنظیم می کند. با رشد روز افزون سیستم های قدرت بهم پیوسته،، کنترل فرکانس بار، اهمیت بیشتری پیدا نموده است و با بهره گیری از روش های جدید، بهره برداری از این سیستم ها را مقدور ساخته است. و هم اکنون نیز پایه بسیاری از مفاهیم پیشرفته برای کنترل سیستم های بزرگ است.
به منظور عملکرد رضایت بخش یک سیستم قدرت ثبات فرکانس امری الزامی است، چرا که کنترل نسبتا دقیق فرکانس ثبات سرعت موتورهای سنکرون و القایی را به دنبال دارد و تثبیت سرعت بارهای موتوری، به طور ویژه در عملکرد رضایت بخش واحدهای تولید اهمیت دارد زیرا این واحدها به شدت به عملکرد تمامی محرک های جنبی مربوط به سوخت، آب و سیستم های تغذیه هوای احتراق وابسته اند.
همچنین در یک شبکه ممکن است افت زیاد فرکانس منجر به ایجاد جریان های شدید مغناطیسی در موتورهای القایی و ترانسفورماتورها شود و صدمات جبران ناپذیری وارد نماید از طرفی استفاده وسیع از ساعت های الکتریکی سنکرون و استفاده از فرکانس برای سایر مصارف زمان سنجی، نیازمند نگهداری و حفظ دقیق زمان سنکرون است که با انتگرال فرکانس متناسب است در نتیجه نه تنها فرکانس، بلکه انتگرال آن نیز باید تنظیم و کنترل شود.
در صورت كاهش بار و اضافه بودن تولید، ژنراتور تمایل به افزایش سرعت و فركانس خود دارد. و در صورت افزایش بار و كمبود تولید، سرعت و فركانس ژنراتور رو به كاهش میرود.
ثبات فرکانس یک سیستم قدرت بستگی به تعادل توان حقیقی دارد و از آنجا که فرکانس عامل مشترکی در سرتاسر سیستم است، هر تغییری در تقاضای توان حقیقی یک نقطه به شکل تغییر فرکانس در سرتاسر سیستم منعکس می شود. و نظر به اینکه توان مورد نیاز یک سیستم قدرت بزرگ، توسط تعداد زیادی ژنراتور تامین می شود باید تغییر توان مورد تقاضا را بین واحدها تقسیم نمود. البته تقسیم بار بین ژنراتورها و کنترل اولیه سرعت توسط گاورنرهای نصب شده بر روی ژنراتورها صورت می پذیرد، لیکن جهت تنظیم دقیق فرکانس در مقدار نامی، نیاز به یک کنترل تکمیلی می باشد که باید در یک مرکز کنترل اصلی انجام شود.
مراکز مدرن کنترل انرژی (Energy Control Center (ECC که با شکبه های رایانه ای به هنگام تجهیز شده اند، پردازش اطلاعات و کنترل را توسط اخذ داده از واحدهای دور، تحت عنوان سیستم SCADA انجام می دهند.
روش های ارائه شده برای کنترل ژنراتورهای مجزا و نهایتا کنترل سیستم های به هم پیوسته بزرگ نقش حیاتی در مراکز مدرن کنترل انرژی ایفا می نمایند. در همین راستا تاکنون تحقیقات زیادی در این خصوص صورت گرفته است.
در یک سیستم قدرت بهم پیوسته تجهیزات، کنترل فرکانس بار و کنترل خودکار ولتاژ بر روی هر ژنراتور نصب می شود. شکل شماتیک حلقه، کنترل فرکانس بار و حلقه تنظیم خودکار ولتاژ یک ژنراتور را نشان می دهد.
کنترل کننده ها برای کار تحت شرایط مشخصی تنظیم شده اند و در مقابل تغییرات کوچک بار، ولتاژ و فرکانس را کنترل می نمایند. تغییرات کوچک در توان حقیقی عمدتا بستگی به تغییر در زاویه روتورها و به تبع آن فرکانس دارد. توان راکتیو نیز وابسته به اندازه ولتاژ (یا به عبارتی تحریک ژنراتور) است. بنابراین با توجه به اینکه تزویج بین حلقه AVR و LFC ناچیز است و همچنین ثابت زمانی سیستم تحریک بسیار کوچکتر از ثابت زمانی محرک ژنراتور (عمدتا توربین ها) می باشد، حالت گذرای آن بسیار سریعتر ازآن است که بر روی دینامیک LFC تاثیر بگذارد.
لذا عموما کنترل فرکانس بار و کنترل تحریک به صورت جداگانه مورد بررسی واقع می شوند. اهداف عمده، کنترل فرکانس بار عبارتند از؛ حفظ فرکانس به صورت یکنواخت، تقسیم بار سیستم بین ژنراتورها به نحو مطلوب و ترجیحا اقتصادی و تنظیم توان مبادله شده از خطوط ارتباطی در مقادیر برنامه ریزی شده می باشند. در واقع می باید تغییر ایجاد شده در فرکانس سیستم و توان حقیقی خطوط ارتباطی توسط تغییر تولید از بین برود. سیگنالهای خط یا به عبارتی![]() تقویت شده و ترکیب می گردد و سپس به سیگنال فرمان حقیقی
تقویت شده و ترکیب می گردد و سپس به سیگنال فرمان حقیقی ![]() تبدیل می شوند که باید به محرک اولیه فرستاده شود تا موجب تغییر توان ورودی به نحو مطلوب گردد. بنابراین محرک واحد نیز توان خروجی خودرا به مقدار
تبدیل می شوند که باید به محرک اولیه فرستاده شود تا موجب تغییر توان ورودی به نحو مطلوب گردد. بنابراین محرک واحد نیز توان خروجی خودرا به مقدار ![]() تغییر خواهد داد و باعث می شود که
تغییر خواهد داد و باعث می شود که![]() تا حد مورد نظر ناچیز شوند.
تا حد مورد نظر ناچیز شوند.
در ادامه PowerEN سعی خواهد کرد با استفاده از دو نمونه از سیستمهای كنترل خودکار بار-فركانس شما را بیشتر با این روش ها آشنا سازد در نظر داشته باشید که طراحی سیستم كنترلی آنها بر مبنای تئوری كنترل بهینه میباشد.
برای هر سیستم كنترل معمولاً پایداری مهمترین چیزی است كه باید مشخص شود. اگر سیستم خطی و مستقل از زمان باشد، معیارهای پایداری مختلفی وجود دارد، كه از میان آنها میتوان معیار پایداری نایكوییست و معیار پایداری روث را نام برد. ولی برای سیستم غیرخطی، یا خطی و متغیر بازمان این معیارها قابل اعمال نیستند.
ما در اینجا روش دوم لیاپانوف را (كه روش مستقیم لیاپانوف خوانده میشود) استفاده خواهیم كرد. این روش عامترین روش تعیین پایداری سیستمهای غیرخطی و یا متغیر با زمان است. صد البته میتوان این روش را برای تحلیل پایداری سیستمهای خطی و مستقل از زمان نیز به كار برد. همچنین در حل مسائل كنترل بهینه درجه دوم كه مورد بحث ما میباشد، نیز روش دوم به كار می آید.
در ابتدا اصول اساسی كنترل بهینه درجه دو را مطرح خواهیم كرد و در ادامه به بررسی دو نمونه سیستم كنترل فركانس-بار خواهیم پرداخت كه در طراحی آنها از كنترل بهینه بهره گرفته شده است.
در این پست تخصصی پس از معرفی مدل ریاضی مناسب برای هر یک از قسمت های سیستم و استخراج معادلات حالت در قسمت اول، با معرفی کنترل بهینه درجه دو و معادله ریکاتی در قسمت دوم، یک کنترل کننده مقاوم بر اساس بحث رابطه ریکاتی در قسمت سوم، معرفی می شود. قسمت اصلی این پروژه یک بحث کامل در مورد روش کنترل بهینه برای، کنترل فرکانس بار سستم های قدرت در قسمت چهارم است. در این قسمت ابتدا، طرح LFC معمول، سپس طرح LFC پیشنهادی به وسیله کنترل کننده (Proportional Integral Diffrential (PID اصلاح یافته معرفی می شود. همچنین در پایان مشکل نویز در طرح LFC و آنالیز کنترل انرژی اضافی نیز مورد بررسی قرار می گیرد.
برای هر سیستم كنترل معمولاً پایداری مهمترین چیزی است كه باید مشخص شود.
اولین مرحله در تحلیل و طراحی یک سیستم کنترل ارائه مدل ریاضی مناسب برای سیستم است. دو روش که اغلب مورد استفاده واقع می شوند عبارتند از: روش تابع انتقال و روش متغیر حالت.
روش متغیر حالت می تواند هم برای سیستم های خطی وهم غیر خطی مورد استفاده قرار گیرد. جهت استفاده از تابع انتقال و معادلات حالت خطی باید معادلات سیستم حول نقطه کار، خطی شوند. در این قسمت ابتدا سیستم را با روش تابع انتقال، مدل و مطالعه می کنیم و سپس با استفاده از آن معادلات حالت را استخراج می نمائیم.
مدل سازی سیستم فرکانس بار
در این قسمت ابتدا با در نظر گرفتن فرضیات و تقریب های مناسب ژنراتور منفردی كه یک ناحیه برق رسانی محلی را تغذیه می کند، مدل می کنیم و سپس بررسی خود را به چندین ژنراتور که همگی قسمتی از یک ناحیه می باشند، گسترش خواهیم داد و آن گاه اتصال نواحی قدرت به یکدیگر را نیز مطالعه خواهیم نمود.
مدل ژنراتور
معادله نوسان یک ماشین سنکرون، به ازای اغتشاش کوچک عبارت است از:
![]() (1-2)
(1-2)
که در آن H ثابت اینرسی ماشین در قدرت مبنای سیستم است.
![]()
به ترتیب تجهیزات توان مکانیکی ورودی و توان الکتریکی خروجی ژنراتور، وات می باشد. زاویه قدرت بر حسب رادیان الکتریکی و ![]() نیز سرعت زاویه ای بر حسب رادیان الکتریکی بر ثانیه است. معادله (1-2) به ازای انحراف کوچک در سرعت به صورت معادله(3-2)نوشته می شود:
نیز سرعت زاویه ای بر حسب رادیان الکتریکی بر ثانیه است. معادله (1-2) به ازای انحراف کوچک در سرعت به صورت معادله(3-2)نوشته می شود:
 (3-2)
(3-2)
و با قرار دادن فرکانس به جای سرعت زاویه ای داریم:
 (3-2)
(3-2)
که در آن ![]() فرکانس نا می سیستم بر حسب
فرکانس نا می سیستم بر حسب ![]() می باشد.
می باشد.
پس از ساده سازی شاهد شکل 1-2 خواهیم بود که در زیر به صورت بلوک نشان داده شده است[1].
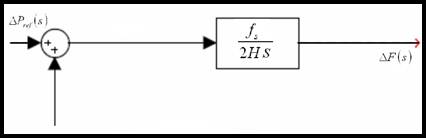
شکل 1-2 نمایش بلوکی ژنراتور
مدل بار
بار یک سیستم قدرت در برگیرنده طیف وسیعی از ادوات الکتریکی برای بارهای مقاومتی از قبیل بارهای روشنای و گرمایی می باشد در این حالت توان الکتریکی مستقل از فرکانس می باشد. اما بارهای موتوری به تغییر در فرکانس حساس می باشند و این که چقدر به فرکانس حساسیت دارند، بستگی به ترکیب مشخصه های بار و سرعت همگی آنها دارد.
تغییرات بار غیر حساس به فرکانس است و![]() ، تغییرات بار حساس به فرکانس را نشان می دهد.
، تغییرات بار حساس به فرکانس را نشان می دهد.
D مطابق رابطه (7-2) تعریف می شود:
![]() (7-2)
(7-2)
با فرض این که ![]() نسبت به فرکانس به صورت خطی تغییر می کند، D برابر است با درصد تغییر در بار نسبت به درصد تغییر در فرکانس.
نسبت به فرکانس به صورت خطی تغییر می کند، D برابر است با درصد تغییر در بار نسبت به درصد تغییر در فرکانس.
برای مثال اگر بار به ازای یک درصد تغییر در فرکانس، 1.6 درصد تغییر کند، D مساوی 1.6 خواهد بود.
به انضمام مدل بار، به نمایش بلوکی ژنراتور و حذف شاخه ی پس خور، به نمایش بلوکی نشان داده شده در شکل 2-2 می رسیم[1].
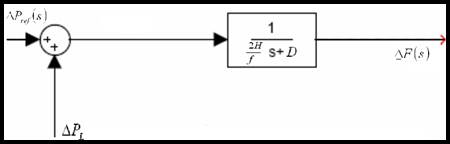
شکل 2-2 نمایش بلوکی بار و ژنراتور
مدل محرک
منبع توان مکانیکی که عموما تحت عنوان محرک اولیه شناخته می شود می تواند توربینهای آبی نصب شده در آبشار ها و رودخانه ها باشد و یا توربین های بخار كه انرژی آنها از طریق سوزاندان زغال گاز و یا سوخت هسته ای تامین می گردد. مدل توربین باید تغییرات توان مکانیکی خروجی را به تغییر موقعیت شیر بخار مرتبط نماید. توربین های مختلف از نظر مشخصات بسیار متنوع اند. ساده ترین مدل محرک اولیه مدل توربین بخار بدون پیش گرمایش است که سیستمی از درجه یک با ثابت زمانی ![]() می باشد و به صورت تابع انتقال زیر نشان داده می شود.
می باشد و به صورت تابع انتقال زیر نشان داده می شود.
(8-2) ![]()
ثابت زمانی ![]() در حدود 0.3 تا 2 ثانیه می باشد تابع تبدیل انواع دیگر توربین ها بسیار پیچیده تر هستند. نمایش بلوکی یک توربین ساده در شکل 3-2 ارائه گردیده است[1].
در حدود 0.3 تا 2 ثانیه می باشد تابع تبدیل انواع دیگر توربین ها بسیار پیچیده تر هستند. نمایش بلوکی یک توربین ساده در شکل 3-2 ارائه گردیده است[1].
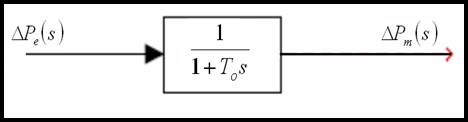
شکل 3-2 نمایش بلوکی یک توربین بخار ساده
مدل گاورنر سرعت
هنگامی که بار الکتریکی ژنراتور به طور ناگهانی افزایش می یابد توان الكتریكی بیشتر از توان مکانیکی ورودی خواهد شد و این کمبود توان مکانیکی توسط انرژی جنبشی ذخیره شده در سیستم دوار رتور جبران خواهد شد، اما کاهش انرژی جنبشی منجر به کاهش سرعت توربین و به تبع آن کاهش فرکانس ژنراتور خواهد شد. تغییر سرعت توسط گاورنر توربین حس خواهد شد و گاورنر دریچه ورودی توربین را طوری تنظیم می کند که توان مکانیکی خروجی توربین به مقدار کافی افزایش پیدا نماید، تا سرعت به یک حالت دائمی جدید برسد.
ابتدایی ترین گاورنرها که به گاورنر وات معروف اند سرعت ژنراتور را توسط گوی های چرخان حس می نمایند و به ازای تغییر سرعت یک جابجایی مکانیکی ایجاد می نمایند. اگر چه امروزه گاورنرهای پیشرفته که اکثرا جهت حس کردن تغییرات سرعت از ادوات الکترونیکی استفاده می کنند، موجود می باشند اما گاورنر فوق همچنان در بسیاری از سیستم های قدرت به کار گرفته می شود.
ابتدایی ترین گاورنرها که به گاورنر وات معروف اند سرعت ژنراتور را توسط گوی های چرخان حس می نمایند و به ازای تغییر سرعت یک جابجایی مکانیکی ایجاد می نمایند.
اجزای سیستم گاورنر
به طور کلی یک سیستم گاورنر در برگیرنده قسمتهای اصلی زیر می باشد:
حس کننده سرعت
این قسمت اساسی شامل گوی های گردانی می باشد که به صورت مستقیم یا توسط چرخ دنده به محور توربین متصل اند و این مکانیزم، متناسب با تغییرات سرعت یک جابجایی مکانیکی ایجاد می شود (حرکت رو به بالا در پاسخ به کاهش سرعت و رو به پایین در پاسخ به افزایش سرعت).
مکانیزم اتصال
این مکانیزم شامل اتصالاتی جهت انتقال جابجایی ایجاد شده توسط گوی های چرخان به شیر ورودی توربین از طریق یک تقویت کننده هیدرولیک و همچنین تهیه یک پس خور ازجابجایی شیر بخار توربین می باشد.
تقویت کننده هیدرولیک
با توجه به این که جابجایی شیر بخار به نیروی مکانیکی خیلی زیادی احتیاج دارد لذا لازم است که جابجایی گاورنر با چند مرحله تقویت هیدرولیک به یک نیروی مکانیکی قوی تبدیل گردد.
تغییر دهنده سرعت
تغییر دهنده ی سرعت شامل یک سروو سیستم است که می تواند به صورت دستی یا خودکار جهت برنامه ریزی فرکانس عمل نماید و با تنظیم این نقطه می توان به توزیع بار دلخواه در فرکانس نامی دست یافت.
به منظور عملکرد پایدار، گاورنر ها طوری طراحی می شوند که با افزایش بار به ژنراتور اجازه افت سرعت دهند.
مکانیزم گاورنر سرعت به صورت یک مقایسه گر عمل می کند خروجی آن، ![]() برابر تفاوت بین توان تنظیم شده مرجع
برابر تفاوت بین توان تنظیم شده مرجع ![]() و توان
و توان ![]() (که توسط مشخصه گاورنر سرعت داده می شود) می باشد.
(که توسط مشخصه گاورنر سرعت داده می شود) می باشد.
![]() (9-2)
(9-2)
به عبارت دیگر:
![]() (10-2)
(10-2)
فرمان ![]() از طریق تقویت کنننده هیدرولیک به فرمان تغییر موقعیت شیر بخار تبدیل می شود. با در نظر گرفتن یک رابطه خطی و یک ثابت زمانی
از طریق تقویت کنننده هیدرولیک به فرمان تغییر موقعیت شیر بخار تبدیل می شود. با در نظر گرفتن یک رابطه خطی و یک ثابت زمانی ![]() برای تقویت کننده هیدرولیک، رابطه زیر را در حوزه لاپلاس خواهیم داشت[1].
برای تقویت کننده هیدرولیک، رابطه زیر را در حوزه لاپلاس خواهیم داشت[1].
![]() (11-2)
(11-2)
معادلات فوق در قالب نمایش بلوکی شکل 4-2 نشان داده شده است.
. 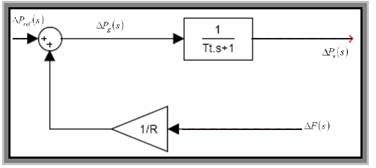
شکل 4-2 نمایش بلوكی سیستم تنظیم سرعت
مدل سیستم فرکانس بار
با تنظیم نمایش بلوکی اشکال 2-2 الی 4-2 و 7-2 و معرفی پارامترهای ![]() در رابطه (13-2) به نمایش بلوکی کامل، کنترل فرکانس بار یک واحد سیستم قدرت مجزا، دست پیدا می کنیم که در شکل 5- 2نشان داده شده است.
در رابطه (13-2) به نمایش بلوکی کامل، کنترل فرکانس بار یک واحد سیستم قدرت مجزا، دست پیدا می کنیم که در شکل 5- 2نشان داده شده است.
![]() (12-2)
(12-2)
![]() (13-2)
(13-2)
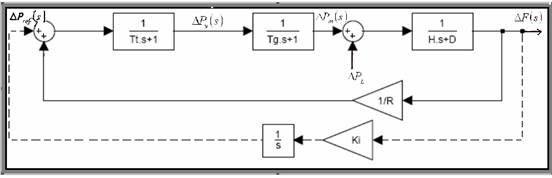
شکل 5-2 نمایش بلوکی کامل فرکانس بار یک سیستم مجزا
مدل سازی عناصر غیر خطی در فرکانس بار
برخی از عناصر موجود در سیستم فرکانس بار به صورت غیر خطی می باشند و با توجه به اینکه این موارد در پایداری سیستم نقش مهمی ایفا می کنند، مورد بررسی قرار خواهند گرفت.
یکی از مهمترین آثار غیر خطی موجود در سیستم وجود باند مرده در گاورنر ها می باشد که در اثر برخی چرخ دنده ها و تقویت کننده های هیدرولیک و اصطحکاک موجود در سیستم مکانیکی ایجاد می گردد. وجود این بانده مرده باعث می شود تا هنگامی كه اندازه سیگنال ورودی به یك مقدار خاص نرسد، سیستم گاورنر پاسخی در خروجی نداشته باشد و در واقع گاورنر به ازای تغییرات سرعتی که کمتر از مقدار باند مرده هستند، هیچ عکس العمل از خود نشان نمی دهد.
محدودیت افزایش تولید در واحدها یکی دیگر از جلوه های غیر خطی در سیستم فرکانس بار است. به بیان دیگر، افزایش یا کاهش تولید انرژی با توجه به سقف حداکثر و حداقل تولید واحدها، محدود می باشد. چرا که از نظر عملی، توان تولیدی، تنها می تواند با حداکثر سرعت مشخصی تغییر کند و این حدود سرعت به این جهت در نظر گرفته شده اند که از نظر انحرافات گسترده متغییرهای پروسه از قبیل دما و فشار (جهت ایمنی سیستم) اجتناب شود.
نمایش بلوکی شکل 6-2 مدل عناصر غیر خطی مذکور را در سیستم فرکانس بار نشان می دهد معمولا اندازه باند مرده را %0.06 در نظر می گیرند. همچنین حداکثر نرخ تولید برای توربین های بخار بدون پیش گرمایش 10% و برای توربین های با پیش گرمایش 3% است.
یکی از مهمترین آثار غیر خطی موجود در سیستم وجود باند مرده در گاورنر ها می باشد که در اثر برخی چرخ دنده ها و تقویت کننده های هیدرولیک و اصطحکاک موجود در سیستم مکانیکی ایجاد می گردد.
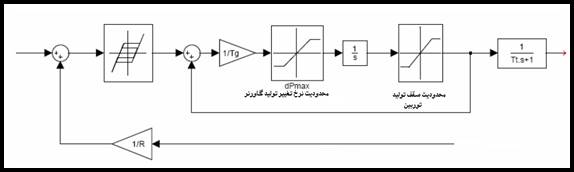
شکل 6-2: نمایش بلوکی عناصر خطی سیستم بار-فرکانس
پاسخ سیستم کنترل فرکانس بار
نظر به اینکه تغییر بار در سیستم قدرت، عموما با قطع یا وصل مقادیر ثابت صورت می پذیرد، در مطالعه سیستم فرکانس بار جهت مدل کردن تغییرات بار از ورودی پله استفاده می شود. برای تحلیل پاسخ سیستم LFC به تغییر بار پله ای، ابتدا حالتی را در نظر می گیریم که تغییر دهنده سرعت در وضعیت مشخصی قرار دارد[2]. ![]() .
.
با توجه به شکل 5-2 رابطه خروجی سیستم کنترل ![]() در حالتی که
در حالتی که ![]() است، به صورت زیر می باشد:
است، به صورت زیر می باشد:
(14-2) 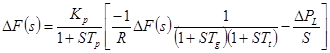
و با توجه به قضیه مقدار نمایی پاسخ ماندگار سیستم عبارت است از:
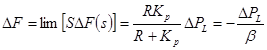 (15-2)
(15-2)
این رابطه، تغییرات فرکانس را بر اثر تغییرات بار نشان می دهد. مخرج رابطه به عنوان مشخصه پاسخ فرکانس منطقه (شامل ژنراتور و بار) مطابق رابطه (16-2) تعریف می شود:
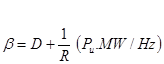 (16-2)
(16-2)
همانگونه که از رابطه (14-2) پیدا است در صورتی که ![]() باشد تغییر ایجاد شده در فرکانس هیچ گاه صفر نخواهد شد. چرا که D از مشخصات بار است و R نیز به دلایل پایداری نمی تواند خیلی کوچک باشد.
باشد تغییر ایجاد شده در فرکانس هیچ گاه صفر نخواهد شد. چرا که D از مشخصات بار است و R نیز به دلایل پایداری نمی تواند خیلی کوچک باشد.
در واقع هنگامی که بار سیستم افزایش می یابد، سرعت توربین، قبل از آنکه گاورنر بتواند بخار ورودی برای بار جدید را تنظیم کند، افت خواهد نمود و این افت سرعت که به منزله افت فرکانس سیستم است، منجر به کاهش بار خواهد شد. بنابراین بار افزوده شده به سیستم، توسط دو مولفه جبران می شود. یکی افزایش تولید و دیگری کاهش کلی بار سیستم در اثر کاهش فرکانس، لذا فرکانس سیستم به مقدار نامی بر نمی گردد.
اما اگر همزمان با تغییر پله ای بار تغییر دهنده سرعت نیز به صورت پله ای تغییر کند پاسخ سیستم کنترل برابر است با:
(17-2) ![]()
بنابراین با تغییر بار می توان تغییر دهنده سرعت را طوری کنترل کرد که ![]() و در نتیجه فرکانس نهایی سیستم به ازای تغییر بار را به مقدار نامی رساند.
و در نتیجه فرکانس نهایی سیستم به ازای تغییر بار را به مقدار نامی رساند.
کنترل کامل سیستم فرکانس بار
برای اینکه فرکانس سیستم ثابت نگه داشته شود باید به ازای تغییر پله ای بار، انحراف فرکانس حالت دائمی یعنی ![]() به صفر برسد و همانطور که دیده شد جهت دستیابی به این هدف باید از تغییر دهنده سرعت استفاده شود تاکنون تحقیقات بسیاری در راستای کنترل تنظیم کننده سرعت جهت نیل به هدف مذکور انجام گرفته است. لیکن روش متداول برای رساندن فرکانس به مقدار نامی، استفاده از یک انتگرال گیر به صورت حلقه پس خود دوم می باشد. زیرا واحد انتگرال خطای میانگین را برای یک دوره زمانی در نظر می گیرد و می تواند آن را به طور کامل حذف کند[2].
به صفر برسد و همانطور که دیده شد جهت دستیابی به این هدف باید از تغییر دهنده سرعت استفاده شود تاکنون تحقیقات بسیاری در راستای کنترل تنظیم کننده سرعت جهت نیل به هدف مذکور انجام گرفته است. لیکن روش متداول برای رساندن فرکانس به مقدار نامی، استفاده از یک انتگرال گیر به صورت حلقه پس خود دوم می باشد. زیرا واحد انتگرال خطای میانگین را برای یک دوره زمانی در نظر می گیرد و می تواند آن را به طور کامل حذف کند[2].
خطوط خط چین در شکل 2-8 نحوه استفاده از انتگرال گیر در سیستم فرکانس بار را نشان می دهد. می توان مشاهده نمود که سیگنال خطای فرکانس پس از تقویت توسط بهره انتگرالی ![]() از طریق انتگرال گیر با فرمان
از طریق انتگرال گیر با فرمان ![]() ایجاد می نماید.
ایجاد می نماید.
 (18-2) و (19-2)
(18-2) و (19-2)
با اعمال قضیه مقدار نهایی:
![]()
پس حلقه پس خور دوم با افزایش درجه سیستم، خطای نمایی فرکانس را صفر می کند. اما دینامیک پاسخ سیستم بستگی به ریشه های معادله درجه دو مخرج رابطه (19-2) دارد. با بررسی این معادله مشخص می شود که با افزایش مقدار ![]() سرعت پاسخ بهتر شده درنتیجه نوسانات افزایش می یابند (در صورت افزایش بیش از اندازه
سرعت پاسخ بهتر شده درنتیجه نوسانات افزایش می یابند (در صورت افزایش بیش از اندازه ![]() ،ممکن است سیستم ناپایدار شود) و کاهش آن منجر به کند شدن پاسخ می گردد. لذا بهره انتگرالی باید طوری تنظیم شود که حالت گذاری مناسبی برای پاسخ ایجاد نماید.
،ممکن است سیستم ناپایدار شود) و کاهش آن منجر به کند شدن پاسخ می گردد. لذا بهره انتگرالی باید طوری تنظیم شود که حالت گذاری مناسبی برای پاسخ ایجاد نماید.
کنترل خودکار تولید (AGC)
همانگونه که قبلا ذکر شد جهت تثبت فرکانس، تغییرات بار نیز به صورت
خود کار طوری تنظیم می شود که فرکانس را به مقدار نامی برگرداند، که این روش به کنترل خودکار تولید یا AGC معروف است[1].
در یک سیستم به هم پیوسته شامل چند ائتلاف نقش AGC عبارت است از تقسیم بار ها در میان واحد ها به گونه ای که فرکانس به صورت یکنواخت حفظ شود و بیشترین کارایی اقتصادی به دست آید. البته کاملا واضح است که سیستم در حالت پایدار فرض شده است و حالت دائمی قابل دستیابی است. در خلال اغتشاشات بزرگ و حالت اضطراری سیستم AGC از مدار خارج می شود و سایر کنترل های اضطراری در سیستم عمل خواهند نمود.
سیستم AGC تغییرات تولید در سیستم را با فرستادن سیگنال هایی به واحد های تحت کنترل خود واقعیت می بخشد. طراحی و عملکرد یک سیستم AGC به شدت وابسته به این است که واحد ها به چنین سیگنال هایی چگونه پاسخ می دهند. مشخصات پاسخ واحد ها به طور وسیعی متغیراند و به عوامل بسیاری بستگی دارند که از جمله می توان به نوع واحد تولید، نوع سوخت مورد استفاده، نوع کنترل کننده های واحد، نقطه کار و عملکرد اپراتورها اشاره نمود.
نواحی کنترل
در بسیاری از حالات، گروهی از ژنراتوراها به صورت نزدیک به هم و محکمی (از نقطه نظر الکتریکی) به یکدیگر متصل اند و بطور هماهنگ نوسان می کنند و توربین ژنراتورها نیز همان مشخصات را دارند. چنین گروهی از ژنراتورها اصطلاحا همنوا نامیده می شوند. بنابراین می توان حلقه LFC را در نظر گرفت که به یک ناحیه کنترل معروف است[1و 2].
در واقع یک ناحیه کنترل را می توان به صورت یک ژنراتور و یک بار در نظر گرفت که ژنراتور معادل دارای ضریب تنظیم سرعت معادل R بوده و قدرت نامی آن با جمع قدرت های نامی ژنراتورها برابر است. بار معادل نیز از مجموع بارهای منطقه تعیین می گردد.
امروزه اغلب سیستم های قدرت به نواحی مجاور خود متصل هستند و اتصال ایجاد نواحی کنترل، یک سیستم قدرت چند ناحیه ای را به وجود می آورد. در یک سیستم قدرت چند ناحیه ای هر ناحیه کنترل در شرایط عادی، بارهای ناحیه خود را تامین می نماید مگر اینکه با توافق دو منطقه مجاور، قدرت مورد نیاز یک ناحیه دیگر تامین گردد. اتصال نواحی کنترل به یکدیگر علاوه بر همکاری فوق الذکر حاوی مزایای دیگری است که عبارتند از:
تغییرات فرکانس کمتر
با اتصال نواحی کنترل به یکدیگر ابعاد سیستم قدرت افزایش می یابد و روشن است که هر چه سیستم بزرگتر باشد انرژی جنبشی آن نیز بیشتر است. در نتیجه در مواقع افزایش بار قادر به تامین انرژی لحظه ای بیشتری خواهد بود، و تغییرات فرکانس کمتری ایجاد خواهد شد.
کاهش ظرفیت نصب و ذخیره چرخان
یک ناحیه منفرد باید جوابگوی حداکثر بار پیش بینی شده خود باشد، اما در یک سیستم همیاری شامل چند ناحیه کنترل، از آنجا که زمان پیک بار در نواحی مختلف متفاوت است لذا قدرت نصب شده کمتری مورد نیاز خواهد بود. همچنین با توجه به اینکه در صورت لزوم هر ناحیه می تواند از ذخیره چرخان سایر مناطق استفاده کند، هر منطقه ذخیره چرخان کمتری لازم خواهد داشت.
مدل سیستم قدرت یک ناحیه ای
همانگونه که توضیح داده شد، یک سیستم قدرت یک ناحیه ای را می توان با یک واحد، که کلیه بارهای منطقه را تامین می کند معادل سازی کرد. برای بررسی پاسخ فرکانس ناحیه می توان نمایش بلوکی شکل 5-2 را به کار گرفت. در اینجا نحوه به دست آوردن پارامترهای معادل ناحیه ارائه شده است.
اگر یک ناحیه کنترل دارای M ژنراتور با قدرت های نامی ![]() و ضرایب تنظیم سرعت
و ضرایب تنظیم سرعت ![]() باشد و خطای فرکانس حالت ماندگار ناحیه در اثر تغییر بار پله ای
باشد و خطای فرکانس حالت ماندگار ناحیه در اثر تغییر بار پله ای ![]() را با
را با ![]() نشان دهیم. برای هر یک از ژنراتور ما می توان نوشت:
نشان دهیم. برای هر یک از ژنراتور ما می توان نوشت:
![]() (20-2)
(20-2)
البته رابطه فوق قدرت مبنا برای ![]() ، همان قدرت نامی ژنراتور یعنی
، همان قدرت نامی ژنراتور یعنی ![]() می باشد.
می باشد.
در حالت ماندگار ![]() بر حسب PU بر مبنای قدرت ناحیه یعنی
بر حسب PU بر مبنای قدرت ناحیه یعنی ![]() برابر است با:
برابر است با:
(21-2) ![]()
با ترکیب دو رابطه فوق و در نظر داشتن تفاوت قدرت های مبنا خواهیم داشت:
(22-2) ![]()
و اگر قدرت مبنای ناحیه را یک فرض کنیم. (S=1pu):
(23-2) 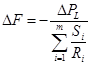
حال اگر ضریب تنظیم سرعت معادل ناحیه را R بنامیم از مقایسه روابط (20-2) و (23-2) خواهیم داشت:
(24-2) 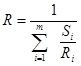
پارامتر معادل H ناحیه نیز از تعریف ثابت اینرسی به صورت زیر به دست خواهد آمد:
(25-2) 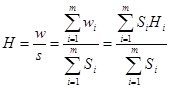
مدل سیستم قدرت دو ناحیه ای
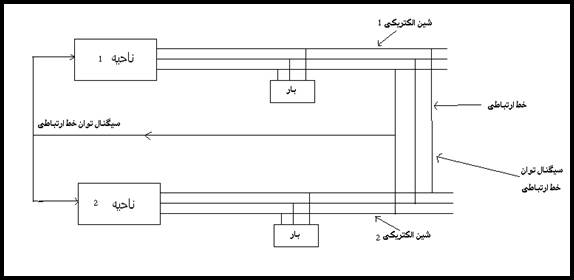
شکل 7-2 نمایش سیستم قدرت دو ناحیه ای
کنترل فرکانس بار یک سیستم چند ناحیه ای را می توان ابتدا با مطالعه یک سیستم دو ناحیه ای آغاز نمود.دو ناحیه کنترل 1و 2 در شکل 7-2 را در نظر بگیرید که توسط یک خط ارتباطی بدون تلفات و بار اکتانس ![]() به یکدیگر متصل شده اند. مطابق شکل 8-2 هر ناحیه توسط یک منبع ولتاژ و راکتانسی معادل بیان می شود. در خلال عملکرد طبیعی، توان حقیقی مبادله شده از طریق خط ارتباطی برابر است با [2]:
به یکدیگر متصل شده اند. مطابق شکل 8-2 هر ناحیه توسط یک منبع ولتاژ و راکتانسی معادل بیان می شود. در خلال عملکرد طبیعی، توان حقیقی مبادله شده از طریق خط ارتباطی برابر است با [2]:
(26-2) ![]()
که در آن ![]()
لذا به ازای انحرافات کوچک توان انتقالی حول مقدار نامی داریم:
(27-2) ![]()
کمیت ![]() شیب منحنی زاویه قدرت در نقطه کار نامی
شیب منحنی زاویه قدرت در نقطه کار نامی ![]() می باشد و ضریب همگام سازی توان نامیده می شود. بنابراین داریم:
می باشد و ضریب همگام سازی توان نامیده می شود. بنابراین داریم:
(28-2) 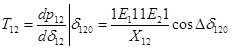
پس انحراف توان خط ارتباطی به فرم زیر در می آید.
(29-2) ![]()
با جایگزینی تغییرات زاویه با تغییرات فرکانس و گرفتن تبدیل لاپلاس از دو طرف رابطه بالا خواهیم داشت:
(30-2) ![]()
با توجه به اینکه از تلفات خط ارتباطی صرف نظر شده است. ![]() و یا برحسب PU داریم:
و یا برحسب PU داریم:
(31-2) ![]()
که ![]() قدرت های نامی نواحی 1و 2 بر حسب MVA می باشند.
قدرت های نامی نواحی 1و 2 بر حسب MVA می باشند.
اگر ضریب ![]() را مطابق (32-2) تعریف کنیم داریم:
را مطابق (32-2) تعریف کنیم داریم:
(32-2) ![]()
(33-2) ![]()
که با وارد کردن توان انتقالی ![]() در نمایش بلوکی منطقه 1 خواهیم داشت:
در نمایش بلوکی منطقه 1 خواهیم داشت:
(34-2) ![]()
و به صورت مشابه برای تغییر فرکانس ناحیه 2 نیز داریم:
(36-2) ![]()
توان جاری از خط ارتباطی به شکل افزایش بار در یک ناحیه و کاهش بار در ناحیه دیگر ظاهر می شود. جهت توان توسط تفاوت زاویه ها تعیین می شود، یعنی اگر ![]() جهت توان جاری شده از ناحیه 1 به ناحیه 2 خواهد بود. نمایش بلوکی سیستم دو ناحیه ای در شکل 8-2 نمایش داده شده است.
جهت توان جاری شده از ناحیه 1 به ناحیه 2 خواهد بود. نمایش بلوکی سیستم دو ناحیه ای در شکل 8-2 نمایش داده شده است.
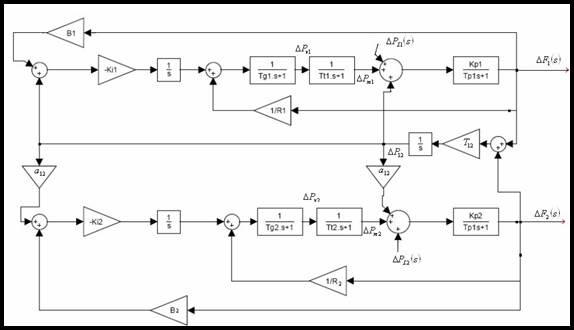
شکل 8-2 نمایش بلوكی كنترل بار فركانس یك سیستم قدرت دو ناحیه ای
کنترل گرایش دار فرکانس خط ارتباطی
همانند سیستم قدرت یک ناحیه ای، جهت حذف کامل خطای فرکانس لازم است که از حلقه کنترل دوم استفاده شود لیکن همانگونه که قبلا اشاره شد در یک ائتلاف چند ناحیه ای سیستم های قدرت، توان های انتقالی از خطوط ارتباطی در حالت دائمی، باید ثابت و برابر مقادیر از پیش تعیین شده باشند. لذا جهت اعمال یک کنترل کامل که هر دو هدف را برآورده سازد باید علاوه بر تغییرات فرکانس از تغییرات توان انتقالی خط ارتباطی نیز پس خور گرفت و ترکیب خطی از دو خط را به عنوان ورودی کنترل کننده در نظر گرفت. این ترکیب خطی را خطای کنترل ناحیه یا (ACE) می نامند و مطابق رابطه (36-2)در هر ناحیه تعریف می شود.
(36-2) ![]()
و بنابراین در صورت استفاده از کنترل کننده انتگرالی خواهیم داشت.
(37-2) 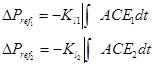
B را ضریب بایاس فرکانس ناحیه می نامند و معمولا مقادیر آن را برابر β یا مشخصه پاسخ فرکانس هر منطقه می گیرند.
سیستم های قدرت چند ناحیه ای
نتایج به دست آمده برای سیستم دو ناحیه ای به سهولت به سیستم چند ناحیه تعمیم داده می شوند.
در یک سیستم قدرت دارای چند ناحیه فرکانس بار، باید اطلاعات قدرت های انتقالی همه خطوط ارتباطی در فواصل زمانی کوتاهی به مرکز کنترل هر ناحیه ارسال شود. سپس جمع این قدرت ها با قدرت تعیین شده در قرار داد نواحی مقایسه گردد تا بتوان خطای کنترل ناحیه را به دست آورد و فرمان کنترل مناسب را به سیستم اعمال نمود نا خطای مذکور به صفر برسد.
نمایش مدل دینامیکی سیستم فرکانس بار به شکل معادلات حالت
همانطور که می دانیم، تمامی روش های کنترل مدل بر مبنای تحلیل سیستم ها به شکل معادلات حالت قرار دارند. لذا در این بخش دینامیک سیستم، کنترل فرکانس بار را با فرض وجود کنترل کننده انتگرالی به صورت معادلات حالت استخراج می نماییم.
معادلات حالت سیستم یک ناحیه ای
ابتدا متغیرهای زیر را به عنوان حالت های سیستم انتخاب می کنیم:
تغییرات فرکانس ![]()
تغییرات توان خروجی توربین ![]()
تغییرات شیر ورودی توربین ![]()
تغییرات نقطه تنظیم سرعت ![]()
با توجه به متغیرهای حالت انتخاب شده و معادلات به دست آمده برای سیستم در قسمت های قبل خواهیم داشت:
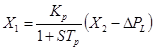
![]() (39-2)
(39-2)
![]()
![]()
و با نوشتن معادلات فوق به صورت در حوزه زمان معادلات حالت سیستم فرکانس بار یک ناحیه کنترل به صورت زیر به دست می آید:
(40-2) ![]()
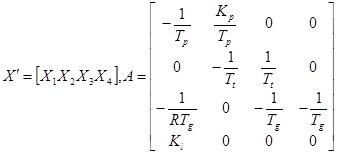
كه درآن:
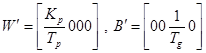
که در آن W بیانگر اغتشاش یا همان تغییر بار سیستم می باشد.
معادلات حالت سیستم دو ناحیه ای
متغیرهای حالت زیر را به عنوان حالت سیستم در نظر می گیریم:
تغییرات فرکانس ناحیه اول ![]()
تغییرات توان مکانیکی خروجی توربین ناحیه اول ![]()
تغییرات شیرورودی توربین ناحیه اول ![]()
تغییرات نقطه تنظیم سرعت ناحیه اول ![]()
تغییرات توان خط ارتباطی بین دو ناحیه ![]()
تغییرات فرکانس ناحیه دوم ![]()
تغییرات توان مکانیکی خروجی توربین ناحیه دوم ![]()
تغییرات شیرورودی توربین ناحیه دوم ![]()
تغییرات نقطه تنظیم سرعت ناحیه دوم ![]()
با استفاده از معادلات سیستم دو ناحیه ای و متغیرهای حالت تعریف شده معادلات حالت سیستم به شکل رابطه (40-2)در می آید که در آن:
![]()
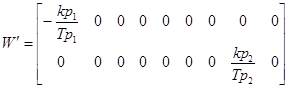

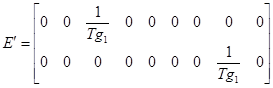
معادلات حالت سیستم چند ناحیه ای
معادلات حالت فرکانس بار سیستم قدرت چند ناحیه ای نیز همانند سیستم دوناحیه ای به شکل رابطه (40-2) بیان می شود.
تمامی روش های کنترل مدل بر مبنای تحلیل سیستم ها به شکل معادلات حالت قرار دارند.
كنترل بهینه درجه دو و معادله ریكاتی
در این قسمت طراحی سیستمهای كنترل پایدار بر اساس شاخصهای عملكرد درجه دو را مطرح میكنیم. سیستمی كه در اینجا در نظر میگیریم، میتوان به صورت زیر تعریف كرد[3]:
| (1-3) |
كه در آن:
x = بردار 1*n
u = بردار 1*n
A = ماتریس ثابت n×n
B = ماتریس ثابت n×r
در طراحی سیستمهای كنترل علاقهمندیم بردار كنترلی (u(t را به نحوی برگزینیم كه یك شاخص عملكرد خاص حداقل شود. میتوان ثابت كرد كه یك شاخص عملكرد درجه دو به صورت
| (2-3) |
كه در آن (L(x,u كه تابعی درجه دو از x و u است، با قواعد كنترلی خطی حداقل میشود. یعنی بردار كنترل به صورت زیر است:
| (3-3) |
كه در آن K ماتریسی r×n به صورت زیر میباشد:
| (4-3) | 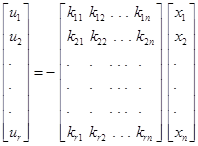 |
بنابراین طراحی سیستمهای كنترل یا تنظیم كننده بهینه بر اساس شاخصهای عملكرد درجه دو، به تعیین درایههای ماتریس K میانجامد. یك مزیت استفاده از كنترل بهینه درجه دو این است كه سیستم طرح شده، بجز در حالتی كه سیستم كنترلپذیر نیست، پایدار است.
در طراحی سیستمهای كنترل بر اساس حداقل كردن شاخصهای عملكرد درجه دو باید معادلات ریكاتی را حل كنیم. MATLAB دستوری بنام lqr دارد كه حل معادله ریكاتی پیوسته در زمان را بدست داده، ماتریس بهره پس خور بهینه را تعیین میكند.
در زیر مسئله تعیین بردار كنترل بهینه (u(t برای سیستم توصیف شده با معادله (1-3) را در نظر میگیریم. شاخص عملكرد عبارت است از
| (5-3) |
كه در آن Q یك ماتریس مثبت معین (یا نیممعین) هرمیتی یا حقیقی معین متقارن، R یك ماتریس مثبت معین هرمیتی یا حقیقی متقارن است، و u بدون قید فرض میشود.
سیستم كنترل بهینه باید شاخص عملكرد را حداقل كند. حل این مسئله روشهای مختلفی دارد، ما در اینجا روشی مبتنی بر روش دوم لیاپانوف ارائه میدهیم.
تذكر این نكته لازم است كه در بحث زیر شاخصهای عملكرد درجه دو مختلط (شاخصهای عملكرد هرمیتی) را برگزیدهایم نه شاخصهای عملكرد درجه دو حقیقی را، زیرا دومی حالت خاصی از اولی است.
توجه داشته باشید که برای سیستمهای دارای بردارها و ماتریسهای حقیقی ![]() به
به ![]() تبدیل میشود.
تبدیل میشود.
بهینهسازی سیستم كنترل با روش دوم لیاپانوف
در روش كلاسیك، سیستم كنترل ابتدا طرح شده، سپس پایداری اش بررسی میشود. روش دیگر این است كه ابتدا شرایط پایداری فرمولبندی شوند و سیستم تحت این محدودیتها طرح شود. اگر طراحی كنترلكننده بهینه بر اساس روش دوم لیاپانوف صورت بگیرد، مطمئنیم كه سیستم كار میكند؛ یعنی خروجی سیستم به طور پیوسته به سمت مقدار مطلوب سوق مییابد. بنابراین سیستم طراحی شده آرایشی دارد كه پایداری، ویژگی ذاتی آن است (اگر سیستم كنترلپذیر نباشد، كنترل بهینه درجه دو قابل اعمال نیست).
برای دسته بزرگی از سیستمهای كنترل میتوان نشان داد كه رابطه مستقیمی بین توابع لیاپانوف و شاخصهای عملكرد درجه دو به كار رفته در طراحی سیستم كنترل بهینه وجود دارد. روش لیاپانوف برای حل مسائل بهینهسازی را با حالت سادهای موسوم به مسئله بهینهسازی پارامتر در ادامه توضیح میدهیم[3].
مسئله بهینهسازی پارامتر به روش دوم لیاپانوف
در زیر رابطه مستقیم بین توابع لیاپانوف و شاخصهای عملكرد درجه دو را مورد بحث قرار میدهیم و مسئله بهینهسازی پارامتر را با استفاده از این رابطه حل میكنیم. سیستم زیر را در نظر میگیریم
| (6-3) |
كه در آن بخش حقیقی مقادیر ویژه ماتریس A منفیاند، یا مبدأ x=0 پایدار مجانبی است. (چنین ماتریسی را ماتریس پایدار مجانبی مینامیم.) فرض میكنیم كه ماتریس A یك یا چند پارامتر قابل تنظیم دارد. میخواهیم شاخص عملكرد زیر را بهینه كنیم
| (7-3) |
كه در آن Q یك ماتریس مثبت معین (یا نیممعین) هرمیتی یا حقیقی متقارن است. بنابراین باید مقادیر پارامترهای قابل تنظیم را به نحوی تعیین كنیم كه شاخص عملكرد حداقل شود.
نشان میدهیم كه میتوان از توابع لیاپانوف به نحوی مؤثر در حل این مسئله استفاده كرد. فرض میكنیم كه:
| (8-3) |
كه در آن Q یك ماتریس مثبت معین است. پس بدست میآوریم:
| (9-3) |
طبق روش دوم لیاپانوف میدانیم كه در صورت پایدار بودن A به ازای Q داده شده یك P وجود داردكه:
| (10-3) |
پس میتوانیم به كمك این معادله درایههای P را تعیین كنیم.
شاخص عملكرد J را میتوان به صورت زیر حساب كرد:
| (11-3) |
چون بخش حقیقی تمام مقادیر ویژه A منفی است، x(∞)→0 . پس داریم:
| (12-3) |
یعنی شاخص عملكرد J را میتوان بر حسب شرط اولیه (x(0 و P بدست آورد. Pطبق روش دوم لیاپانوف به A و Q مرتبط میشود. پس اگر مثلاً بخواهیم یك پارامتر سیستم را برای حداقل كردن شاخص J تنظیم كنیم، میتوانیم ![]() را نسبت به پارامتر مورد نظر حداقل كنیم. چون (x(0 شرط اولیه داده شدهاست و Q نیز دادهشده، P تابعی از درایههای A است. پس این فرایند حداقل سازی به مقدار بهینه پارامتر قابل تنظیم منجر میشود. توجه به این نكته مهم است كه مقدار بهینه این پارامتر در حالت كلی به شرط اولیه (x(0 بستگی دارد.
را نسبت به پارامتر مورد نظر حداقل كنیم. چون (x(0 شرط اولیه داده شدهاست و Q نیز دادهشده، P تابعی از درایههای A است. پس این فرایند حداقل سازی به مقدار بهینه پارامتر قابل تنظیم منجر میشود. توجه به این نكته مهم است كه مقدار بهینه این پارامتر در حالت كلی به شرط اولیه (x(0 بستگی دارد.
كنترل بهینه درجه دو
حال این مسئله كنترل بهینه را در نظر میگیریم؛ سیستم زیر داده شدهاست[4و3]:
| (13-3) |
ماتریس K را برای بردار كنترل بهینه
| (14-3) |
به نحوی تعیین میكنیم كه شاخص عملكرد زیر حداقل شود:
| (15-3) |
Q یك ماتریس مثبت معین (یا نیممعین) هرمیتی یا حقیقی متقارن، R نیز یك ماتریس مثبت معین هرمیتی یا حقیقی متقارن است. توجه كنید كه جمله دوم سمت راست رابطه بالا مصرف انرژی سیگنال كنترل را نشان میدهد. ماتریسهای Q و P اهمیت نسبی خطا و مصرف انرژی را تعیین میكنند. در اینجا فرض میكنیم سیگنال كنترل (u(t بدون قید است. چنانچه خواهیم دید قاعده كنترل خطی بیان شده با معادله ![]() ، قاعده كنترل بهینه است. بنابراین اگر درایههای ماتریس K به نحوی معین شوند كه شاخص عملكرد حداقل شود، در این صورت (u(t به ازای هر شرط اولیهای بهینه است.
، قاعده كنترل بهینه است. بنابراین اگر درایههای ماتریس K به نحوی معین شوند كه شاخص عملكرد حداقل شود، در این صورت (u(t به ازای هر شرط اولیهای بهینه است.
با گذاشتن معادله (14-3) در معادله (13-3) بدست میآوریم:
| (16-3) |
ماتریس A-BK را پایدار فرض میكنیم، یعنی فرض میكنیم مقادیر ویژه آن دارای بخش حقیقی منفی هستند.
با جایگذاری معادله (14-3) در (15-3) بدست میآوریم:
| (17-3) | 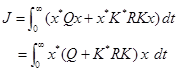 |
برای حل مسئله بهینهسازی پارامتر قرار میدهیم
| (18-3) |
كه در آن P یك ماتریس مثبت معین هرمیتی یا حقیقی متقارن است. پس بدست میآوریم
| (19-3) |
مقایسه دو طرف معادله بالا نشان میدهد كه برای برقراری آن به ازای تمام مقادیر x باید داشته باشیم
| (20-3) |
طبق روش دوم لیاپانوف اگر A-BK ماتریسی پایدار باشد، در این صورت یك ماتریس مثبت معین P وجود دارد كه معادله (20-3) را ارضا كند.
پس باید درایههای P را با توجه به این معادله تعیین كنیم و ببینیم آیا مثبت معین است یا نه.(ممكن است بیش از یك P این معادله را ارضا كند. اگر سیستم پایدار باشد حتماً یك ماتریس مثبت معین وجود دارد كه این معادله را ارضا كند. یعنی اگر این معادله را حل كنیم و یك ماتریس مثبت معین P بدست آوریم، سیستم پایدار است. ماتریسهای Pدیگری را كه این معادله را ارضا میكنند ولی مثبت معین نیستند، باید كنار گذاشت).
شاخص عملكرد J را میتوان به صورت زیر محاسبه كرد[4]:
| (21-3) |
چون بخش حقیقی تمام مقادیر ویژه A-BK منفی است، آنگاه x(∞)→0 ؛ پس بدست میآوریم
| (22-3) |
پس شاخص عملكرد J را میتوان بر حسب شرط اولیه (x(0 و P به دست آورد.
برای یافتن حل مسئله كنترل بهینه درجه دو به این صورت عمل میكنیم؛ چون R را مثبت معین هرمیتی یا حقیقی متقارن فرض كردهایم، میتوانیم بنویسیم:
| (23-3) |
كه T یك ماتریس ناتكین است. پس معادله (20-3) را میتوان به شكل زیر نوشت
| (24-3) |
و آن را به صورت زیر در آورد
| (25-3) |
حداقل كردن J نسبت به K مستلزم حداقل كردن ماتریس زیر نسبت به K است:
| (26-3) |
چون عبارت اخیر غیرمنفی است، حداقل آن به ازای صفر شدن آن حاصل میشود، یعنی وقتی داریم
| (27-3) |
پس
| (28-3) |
معادله (28-3) ماتریس بهینه K را بدست میدهد. پس وقتی شاخص عملكرد به صورت معادله (15-3) است، قاعده كنترل بهینه برای مسئله كنترل بهینه درجه دو خطی به صورت زیر است:
| (29-3) |
ماتریس P معادله (28-3) باید معادله(20-3) یا معادله ساده شده زیر را ارضا كند:
| (30-3) |
معادله (30-3) را معادله ریكاتی ماتریس ساده شده مینامند. پس گامهای طراحی را میتوان به صورت زیر بیان كرد:
1. با حل معادله ریكاتی، ماتریس P را بیابید. (اگر یك ماتریس P مثبت معین وجود داشته باشد سیستم یا ماتریس A-BK پایدار است.)[4]
2. این ماتریس P را در معادله (3-28) قرار دهید. ماتریس K حاصل ماتریس بهینه است.
توجه كنید كه در صورت پایداری ماتریس A-BK این روش همیشه جواب درست میدهد.
روش دیگری نیز برای تعیین ماتریس بهره پس خور بهینه K وجود دارد. گامهای طراحی در این روش عبارتند از:
1. ماتریس P ارضا كننده معادله (3-20) را به صورت تابعی از K تعیین كنید.
2. ماتریس P را در معادله (3-22) قرار دهید. بنابراین شاخص عملكرد تابعی از K میشود.
3. درایههای K را به نحوی تعیین كنید كه شاخص عملكرد J حداقل شود. حداقل كردن J نسبت به درایههای kij ماتریس K با برابر صفر قرار دادن ∂J/∂kij و تعیین مقادیر بهینه kij انجام میشود.
اگر تعداد درایههای kij زیاد باشد این روش مناسب نیست.
حل مسائل كنترل بهینه درجه دو با MATLAB
دستور زیر
مسئله تنظیم كننده خطی پیوسته در زمان مبنی بر معادله ریكاتی را حل میكند. این دستور ماتریس بهره پس خور بهینه K را به نحوی تعیین میكند كه قاعده كنترلی u=-Kx شاخص عملكرد زیر را برای سیستم تعریف شده با![]() حداقل كند.
حداقل كند.
دستور
ماتریس P، یعنی حل یكتای مثبت معین معادله ریكاتی ماتریس ساده شده را نیز بدست میدهد
اگر ماتریس A-BK پایدار باشد، این حل مثبت معین همیشه وجود دارد. این دستور قطبهای حلقه بسته یا مقادیر ویژه A-BK را نیز به دست میدهد.
توجه به این نكته مهم است كه برای بعضی سیستم ها K هر چه انتخاب شود، A-BK پایدار نیست. در این موارد معادله ریكاتی جواب مثبت معین ندارد. در چنین مواردی دستورهای
جواب ندارند و حلی كه MATLAB بدست میدهد عبارت است از:
هرگاه حل مسئله كنترل بهینه درجه دو وجود نداشته باشد، ماتریس K تعیین شده توسط MATLAB دارای(NaN (Not A Numberخواهد بود.
طراحی یك كنترلكننده مقاوم برای كنترل بار-فركانس سیستمهای قدرت
در این قسمت یک کنترل کننده مقاوم بر اساس بحث رابطه Riccati برای کنترل بار-فرکانس سیستمهای قدرت پیشنهاد شدهاست. LFC پیشنهادی ساده و مؤثر است و میتواند اطمینان دهد که سیستم کلّی برای تمام عدم قطعیتها در حضور محدودیت نرخ تولید (GRC) صادق است.
معرفی کنترل کننده مقاوم
کنترل فرکانس بار (LFC) در طراحی و بهرهبرداری از سیستمهای قدرت از اهمیت ویژهای برخوردار است. میزان بارگذاری در یك سیستم قدرت ثابت نمیباشد، لذا برای اطمینان از كیفیت توان در سیستم قدرت، نیازمند به طراحی یك سیستم کنترل فرکانس بار هستیم تا میزان تولید و فركانس ژنراتور را در حد مطلوبی كنترل كند. در طول 20 سال اخیر تلاشهای زیادی انجام گرفته که سیستم LFC با عملکرد بهتری ساخته شود و استراتژیهای كنترلی زیادی از سال 1970 به بعد برای آن ارائه شدهاست.
یک کارخانه صنعتی از قبیل یک نیروگاه قدرت همیشه شامل پارامترهای نامعلوم است که در طراحی کنترلکننده باید مدنظر قرار گیرند. در غیر این صورت، اگر نیروگاه واقعی نسبت به آن چیزی که فرض شده تغییر یابد کنترلکننده طراحی شده توسط روش طراحی کلاسیک ممکن است نتواند پایداری کل سیستم را اطمینان دهد.
اخیراً نویسندگان زیادی به مبحث سیستمهای با ساختار متغیر (VSS) برای طراحی LFC روی آوردهاند. کنترل کننده VSSساختار سیستم را با توجه به بعضی قوانین تغییر ساختاری عوض میکند که عملکرد دینامیکی سیستم را بهبود میبخشد و کنترل کننده را نسبت به تغییرات پارامترها غیرحساس میکند در اینجا یک کنترل کننده فیدبک خطی ثابت مقاوم برای سیستمهای قدرت طراحی شده که از مبحث رابطه Riccati استفاده شدهاست.
کنترل کننده مقاوم پیشنهادی میتواند پایداری کلی سیستم را برای تمام عدم قطعیتهای قابل قبول نوید دهد، حتی در حضور محدودیت نرخ تولید (GRC) عملکرد خوبی را از کنترلکننده پیشنهادی شاهد خواهیم بود.
یک کارخانه صنعتی از قبیل یک نیروگاه قدرت همیشه شامل پارامترهای نامعلوم است که در طراحی کنترلکننده باید مدنظر قرار گیرند.
مدل نیروگاه
سیستمهای قدرت دارای مدل دینامیکی غیرخطی پیچیدهای می باشند، ولی از آنجایی که سیستم قدرت در طی عملکرد معمولی خود فقط تحت تغییرات کوچک بار قرار میگیرد مدل خطیسازی شده میتواند مورد استفاده قرار گیرد و برای نمایش رفتار دینامیکی سیستم قدرت حول نقطه کار کافی خواهد بود.
مبحث طراحی معمول برای LFC از تئوری کنترل خطی برای توسعه قوانین کنترل بر اساس مدل خطی استفاده میکند. با وجود این از آنجا که پارامترهای سیستم به طور کلی نامعلوم هستند کنترل کننده طراحی شده بر اساس یک مدل با پارامترهای ثابت برای نیروگاه حقیقی ممکن است درست کار نکند لذا برای اینکه این پارامترها مدنظر قرار گیرند در این مقاله ما از رابطه Riccati برای طراحی یک LFC مقاوم استفاده میکنیم.
نمایش بلوکی مدل خطی شده نیروگاه در شکل زیر آورده شده است:
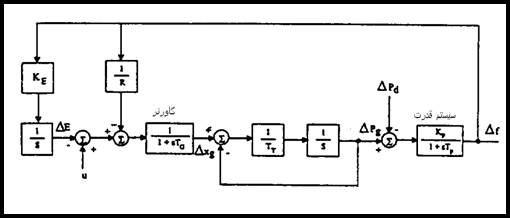
شكل 1-4: نمایش بلوکی سیستم قدرت نمونه
مدلی که ما در اینجا مورد توجه قرار دادهایم میتواند اینگونه نوشته شود:
| (1-4) | 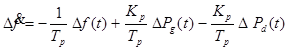 |
| (2-4) | |
| (3-4) |
كه:
![]() : تغییرات افزایشی فرکانس به هرتز؛
: تغییرات افزایشی فرکانس به هرتز؛
![]() : تغییرات افزایشی خروجی ژنراتور به p.u. MW ؛
: تغییرات افزایشی خروجی ژنراتور به p.u. MW ؛
![]() : تغییرات افزایشی موقعی شیرگاورنر؛
: تغییرات افزایشی موقعی شیرگاورنر؛
![]() : تغییرات افزایشی در کنترل انتگرال؛
: تغییرات افزایشی در کنترل انتگرال؛
![]() : اغتشاش بار به p.u. MW ؛
: اغتشاش بار به p.u. MW ؛
![]() : ثابت زمانی گاورنر به ثانیه؛
: ثابت زمانی گاورنر به ثانیه؛
![]() : ثابت زمانی توربین به ثانیه؛
: ثابت زمانی توربین به ثانیه؛
![]() : ثابت زمانی مدل نیروگاه به ثانیه؛
: ثابت زمانی مدل نیروگاه به ثانیه؛
![]() : بهره نیروگاه؛
: بهره نیروگاه؛
![]() : تنظیم سرعت بهHz p.u. MW– ؛
: تنظیم سرعت بهHz p.u. MW– ؛
سیگنال كنترل انتگرالی (∆f(t، به صورت زیر میباشد:
| (4-4) | 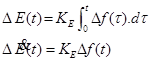 |
كه KE بهره كنترل انتگرالی است.
میتوان مدل مذكور را بر اساس معادلات فضای حالت به صورت زیر بازنویسی كرد:
| (5-4) |
كه:
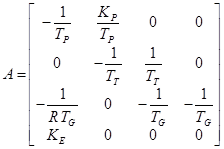 |
|
محدوده تغییر پارامترهای سیستم به صورت زیر میباشد:
كه![]() (i=1,…، ثابتهایی معلوم میباشند.
(i=1,…، ثابتهایی معلوم میباشند.
طراحی كنترل كننده
در مدل نیروگاه بیان شده با رابطه (5-4) مقدار ∆Pd(t)=0 را قرار دهید.
از آنجایی كه پارامترهای سیستم دقیقاً مشخص نیستند، لذا مدل زیر را كه عدم قطعیت را نیز در بر دارد، مورد استفاده قرار میدهیم:
| (6-4) |
ماتریسهای ![]() و
و ![]() ، ماتریسهای ثابت نامی هستند. از ساختار مدل سیستم واضح است كه ماتریس ∆A، عدم قطعیت از بعد یكم میباشد.یعنی:
، ماتریسهای ثابت نامی هستند. از ساختار مدل سیستم واضح است كه ماتریس ∆A، عدم قطعیت از بعد یكم میباشد.یعنی:
![]() ها ماتریسهای ثابت هستند،
ها ماتریسهای ثابت هستند، ![]() ،
، ![]() و
و ![]() . ثابتهای α و
. ثابتهای α و ![]() نیز معلوماند.
نیز معلوماند.
ما میخواهیم کنترلكننده فیدبک خطی ![]() را به گونهای طراحی کنیم که برای تمام عدم قطعیتهای قابل قبول سیستم حلقه بسته کلی به طور مجانبی پایدار باشد.
را به گونهای طراحی کنیم که برای تمام عدم قطعیتهای قابل قبول سیستم حلقه بسته کلی به طور مجانبی پایدار باشد.
به دلیل اینکه rank عدم قطعیتها برابر 1 است، میتوان Ai ها را بصورت زیر نوشت:
| (7-4) |
كه di و ei (i=1, 2, 3) بردارهای ثابت و معلوم میباشند.
در ادامه مباحث مطرح شده در مراجع [5و6]، تعاریف زیر را انجام میدهیم:
| (8-4) | |
| (9-4) |
روش حل مسئله طراحی یک کنترل کننده فرکانس بار مقاوم برای سیستم قدرت شامل حلکردن رابطه جبری معادله ریكاتی زیر است:
| (10-4) |
كه >0 ![]() و
و ![]() و ماتریسهای Qو P ماتریسهای مثبت معین هستند که توسط طراح انتخاب میشوند.
و ماتریسهای Qو P ماتریسهای مثبت معین هستند که توسط طراح انتخاب میشوند.
روش پیشنهادی برای حل رابطه بالا در مراجع [6و7] موجود است، که نتایج زیر از آن قابل حصول اند:
اگر برای برخی از ε,ε1>0 ها، یک جواب مثبت معین برای p در رابطه (10-4) موجود باشد آنگاه سیستم برای تمامی مقادیر عدم قطعیتهای قابل قبول به طور مجانبی پایدار خواهد بود و روابط (7-4) تا (9-4) را توسط قانون فیدبک خطی زیر ارضا میکند:
| (11-4) |
برای اثبات فرض میكنیم كه تابع لیاپانوف به صورت (V(x=xTPx باشد، آنگاه مشتق (V(xبرابر خواهد بود با:
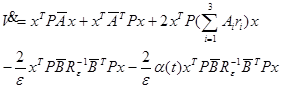 |
حال
كه ![]()
با استفاده از نامساوی فوق داریم:
اگر رابطه (10-4) برقرار باشد، داریم:
توجه كنید كه وقتی پارامتر های سیستم مقادیر نرمال را دارند، بهترین عملکرد سیستم توسط قانون کنترل (11-4) قابل بهرگیری است.
سیستم قدرت (6-4) به طور مجانبی برای تمام مقادیر عدم قطعیت مجاز پایدار است و خواهیم داشت:
در ادامه روش طراحی كنترلكننده پیشنهادی را توضیح خواهیم داد و پاسخ سیستم به تغیر بار ∆Pd(t)=0.01 را مورد مطالعه قرار خواهیم داد.
سیستم مدل شده با معادلات (1-4) تا (4-4) را در نظر می گیریم. فرم كلی معادلات حالت به شكل زیر است:
كه ![]() ،
، ![]() و
و ![]() .
.
اكنون مقادیر نامی پارامترها را مطابق زیر انتخاب می كنیم:
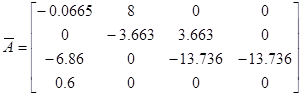 |
|
بازه تغییرات پارامترهای سیستم هم در محدودههای زیر میباشد:
به خاطر عدم قطعیتهای از مرتبه 1، خواهیم داشت:
كه
 |
|
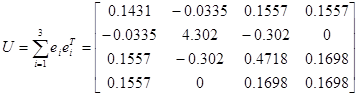 |
و ![]() ؛
؛ ![]() (كه
(كه ![]() ،
، ![]() )
)
با انتخاب ε=1، Q=I، ε1=5 و R=1، حل معادله ریكاتی نتیجه زیر را بدست میدهد:
كه
در طراحی و تحلیل بالا، محدودیت نرخ تولید (GRC) مورد توجه قرار نگرفته است. در یك سیستم قدرت واقعی برای ماكزیمم نرخ تغییر تولید توان، یك محدودیتی وجود دارد. نتایج ذكر شده در مراجع [8و9] به این نكته اشاره دارند كه GRC بطور قابل ملاحظهای پاسخ سیستم قدرت را تحت تأثیر قرار میدهد. سیستمی كه GRC در آن لحاظ شده باشد در قیاس با موردی كه GRC در نظر گرفته نشده است، دارای، فرا جهش وsetting time بزرگتری خواهد بود. بعلاوه از آنجایی كه پارامترهای سیستم دقیقاً شناخته شده نیستند، سیستم كلی ممكن است در حضور اغتشاش بار، ناپایدار شود. در این بخش كارایی کنترل کننده فرکانس بار پیشنهادی را در یك سیستم قدرت با در نظر گرفتن GRC ارزیابی میكنیم. اندازه GRC، 0.1 p.u. در دقیقه در نظر گرفته شدهاست. یعنی:
GRCبا اضافه كردن یك محدود كننده به بلوك توربین مدل میشود. نمایش بلوکی مدل نیروگاه با GRC در شكل زیر نشان داده شده است.
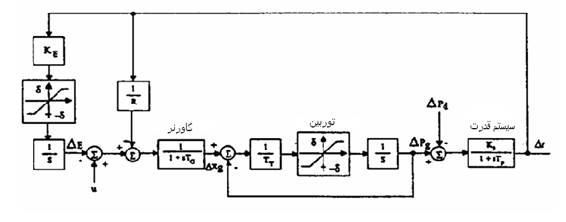
شكل 2-4: نمایش بلوکی سیستم قدرت با در نظر گرفتن GRC
تغییرات بار را 0.01 p.u. فرض كنید، یعنی ∆Pd(t)=0.01.
ابتدا گروههای مختلفی از پارامترهای سیستم را انتخاب میكنیم.
A: با مقادیر پارامترهای نامی
B: ![]()
C: ![]()
نتایج شبیهسازی توسط مؤلف (∆Pg(t و (∆t(t و (∆Xg(t برای كنترلكننده پیشنهادی در شكلهای 3-4 تا 5-4 نشان داده شدهاند. در این شبیهسازیها GRC برابر است با δ=0.0017
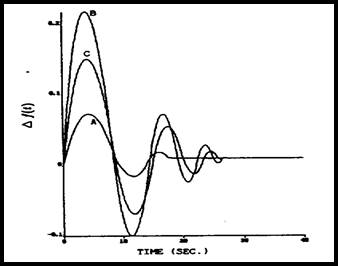
شكل 3-4: پاسخ (∆t(t برای پارامترهای متفاوت
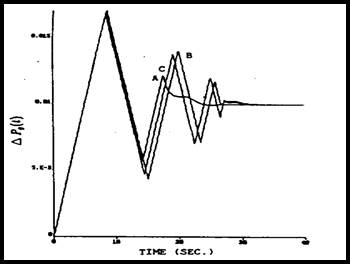
شكل 4-4: پاسخ (∆Pg(t برای پارامترهای متفاوت
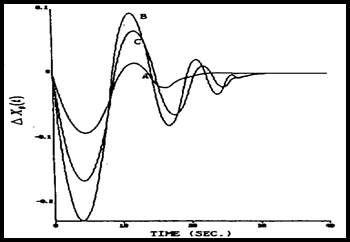
شكل 5-4: پاسخ (∆Xg(t برای پارامترهای متفاوت
حال سیستم با پارامترهای نامی را در نظر بگیرید. شكل 6-4 پاسخ (∆f(t را در حالت با GRC و بدون آن نشان میدهد.
A: با GRC، δ=0.0017؛
B: با GRC، δ=0.0034؛
C: بدون GRC؛
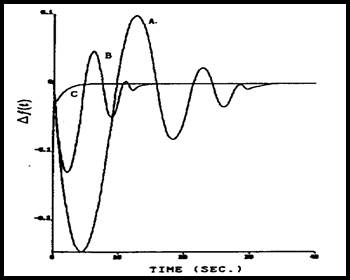
شكل 6-4: پاسخ (∆f(t برای GRC های متفاوت
پارامترهای سیستم را بصورت زیر در نظر بگیرید:
![]()
A: یعنی همه پارامترهای سیستم مقادیر نامی باشند بجز KP كه اندازه آن برابر است با KP=180؛
B: با پارامترهای نامی؛
شكل 7-4 پاسخ (∆f(t را با GRC δ=0.0017 برای دو حالت A و B نشان میدهد.
بررسی نتایج این شبیهسازیها نشان میدهد كنترلكننده پیشنهادی، سیستم قدرت را برای تمام عدم قطعیتهای قابل قبول و با در نظر گرفتن GRC، بطور مجانبی پایدار میسازد. یعنی:
نتایج شبیهسازی در شكل 7-4 نشان میدهد كه پاسخ نیروگاه به بهره نیروگاه KP، نسبت به سایر پارامترها، بسیار حساستر است.
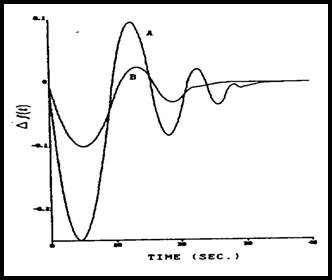
شكل 7-4: پاسخ (∆f(t برای KP های متفاوت
این شبیهسازیها همچنین این نكته را تأیید میكنند كه موقعی كه GRC لحاظ شده باشد سیستم، فرا جهش و setting time بزرگتری را در مقایسه با موردی كه GRC در نظر گرفته نشده باشد، خواهد داشت.
نتایج بدست آمده از شبیهسازی توسط Simulink
شكل 8-4: پاسخ (∆f(t برای سیستم با پارامترهای نامی(گروهA)
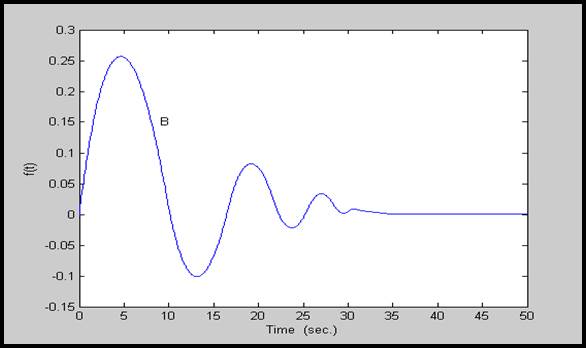
شكل 9-4: پاسخ (∆f(t برای سیستم با پارامترهای گروه دوم (گروه B)
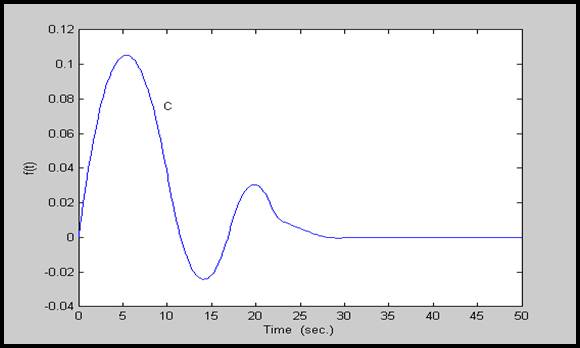
شكل 10-4:پاسخ (∆f(t برای سیستم با پارامترهای گروه سوم(گروه C)
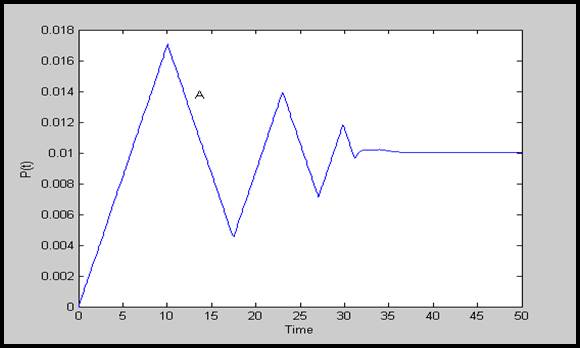
شكل 11-4: پاسخ (∆Pg(t برای سیستم با پارامترهای نامی(گروه A)

شكل 12-4: پاسخ (∆Pg(t برای سیستم با پارامترهای گروه دوم (گروه B)
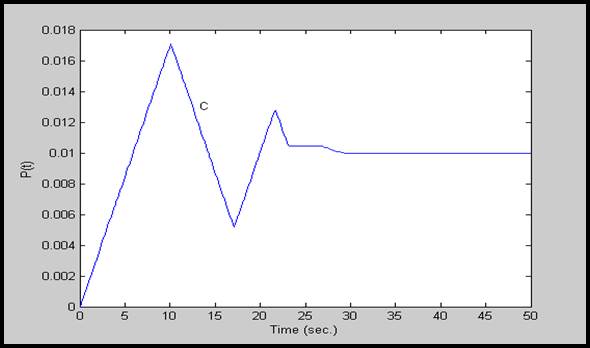
شكل 13-4: پاسخ (∆Pg(t برای سیستم با پارامترهای گروه سوم (گروه C)
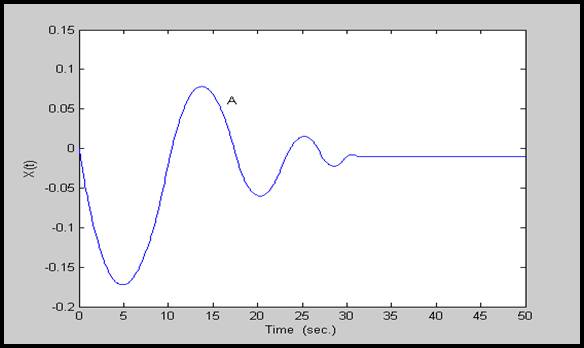
شكل 14-4: پاسخ (∆Xg(t برای سیستم با پارامترهای نامی(گروه A)
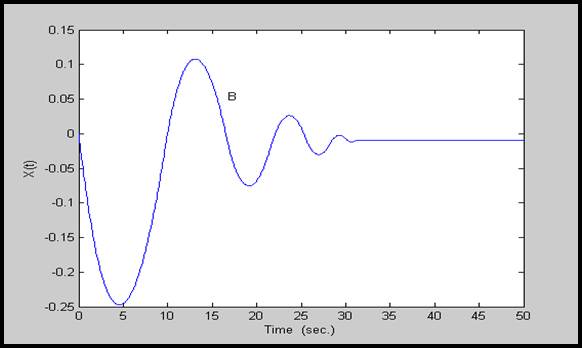
شكل 15-4:پاسخ (∆Xg(t برای سیستم با پارامترهای گروه دوم(گروه B)
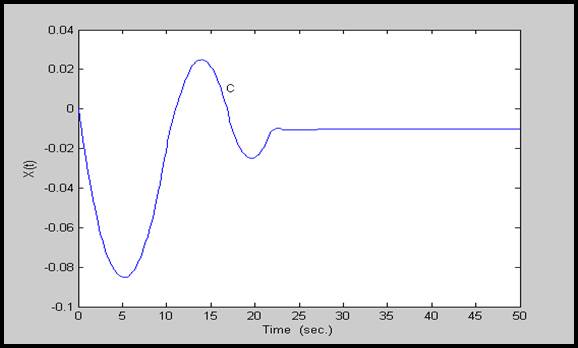
شكل 16-4: پاسخ (∆Xg(t برای سیستم با پارامترهای گروه سوم(گروه C
و برای سیستم با پارامترهای نامی و GRC های مختلف نتایج زیر از شبیهسازی حاصل شده است:
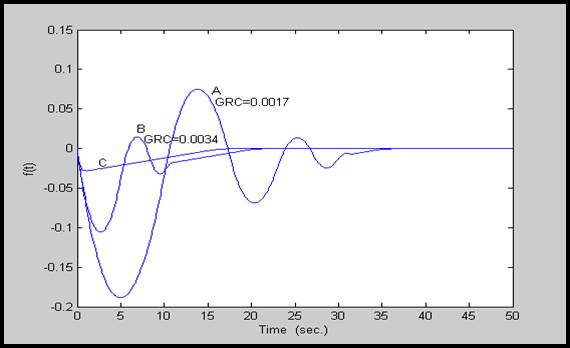
شكل 17-4: پاسخ (∆f(t برای سیستمهای با GRC های متفاوت، و سیستم بدون GRC
سیستم با پارامترهای نامی و KP های مختلف، یكی مقدار نامی KP=120.3 و دیگری KP=180 نتایج زیر را بدست داده است:
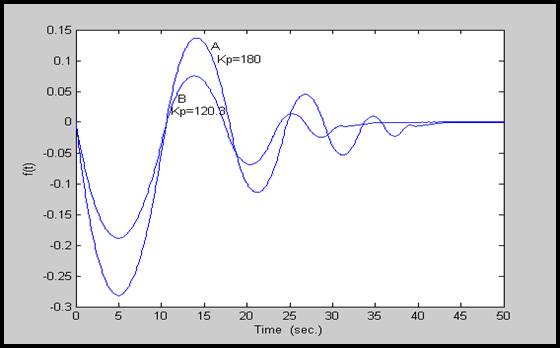
شكل 18-4: پاسخ (∆f(t برای سیستمهای با KP های متفاوت، و پارامترهای نامی
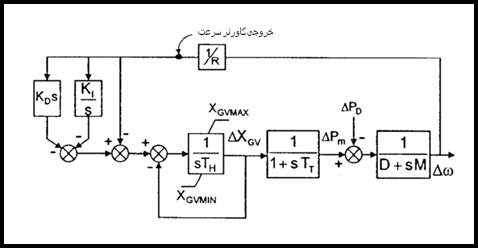
شكل 3-5: نمایش بلوکی طرح LFC پیشنهادی
حالت I: بدون حلقه کنترلی انتگرالی (KL=0)
در این حالت تابع انتقال حلقه باز بوسیله رابط زیر داده می شود.
(4-5) ![]()
مکان هندسی ریشه ها رفتارتساوی بالا با مادیر مختلف ![]() با استفاده از پارامتر های ژنراتور داده شده در جدول آزمایش می شود.
با استفاده از پارامتر های ژنراتور داده شده در جدول آزمایش می شود.
وقتی ![]() ، زاویه های خطوط مجانب، نقاط برخورد آنها با محور آنها با محور اعداد حقیقی و نقاط جدایی روی مکان هندسی ریشه ها به صورت زیر محاسبه می شوند.
، زاویه های خطوط مجانب، نقاط برخورد آنها با محور آنها با محور اعداد حقیقی و نقاط جدایی روی مکان هندسی ریشه ها به صورت زیر محاسبه می شوند.
زاویه های خطوط مجانب 
(5-5) نقاط برخورد θ0=л /2,θ1=3л /2
σc=-6.072 نقاط جدایی
مکان هندسی ریشه های مربوطه در شکل 4-5 الف نمایش داده شده است.
وقتی ![]() ، زاویه های خطوط مجانب نقاط برخورد آنها با محور اعداد حقیقی و نقاط جدایی روی مکان هندسی ریشه هایبه صورت زیر محاسبه می شوند.
، زاویه های خطوط مجانب نقاط برخورد آنها با محور اعداد حقیقی و نقاط جدایی روی مکان هندسی ریشه هایبه صورت زیر محاسبه می شوند.
زاویه های خطوط مجانب θ0=л /2,θ1=3л /2
σA=-5.083 نقاط برخورد (6-5)
σc=-6.072 نقاط جدایی
مکان هندسی ریشه هایمربوطه در شکل 4-5 بنمایش داده شده است.
در اینجا باید توجه شود که در حالت بخصوص قطب ![]() با صفر z1 کنسل شده است.
با صفر z1 کنسل شده است.
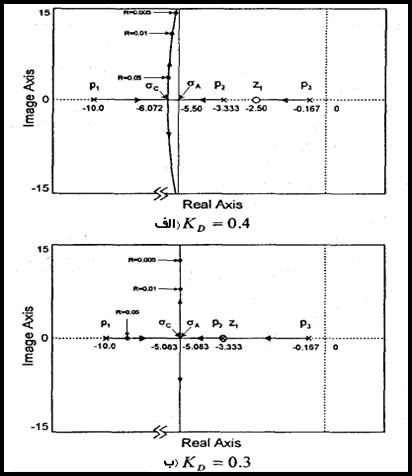
شکل 4-5: مکان هندسی ریشه هایبرای LFC پیشنهادی بدون حلقه انتگرالی
الف: ![]()
ب:( ![]() )
)
همانطور که شکل 4-5 نشان داده شده است مجانب ها به نقاط برخوردشان در سمت چپ صفحه S عمود هستند.
از مکان هندسی ریشه های بالا دریافت می شود که افزایش حلقه پس خور مشتقی دارای اثری است که ازحرکت منحنیمکان هندسی ریشه هایبه سمت نیمه راست صفحۀ S ممانعت به عمل می آورد (با منحنی طرح کنترلی ساده پس خوری در شکل 2-5 مقایسه شود)، مکان هندسی ریشه های بالا نشان می دهد طرح کنترلی پیشنهاد شده رنج تثبیت تنظیم فرکاتس R را منسبط می کند. در اینجا باید توجه شود که انتخاب بهره مشتقی ![]() مجانب عمومی به سمت راست حرکت می کند. اگر بهره مشتقی
مجانب عمومی به سمت راست حرکت می کند. اگر بهره مشتقی ![]() تا مقدار بحرانی خویش کاهش یابد مجانب عمومی روی محور موهومی قرار می گیرد. مقدار بحرانی بهرۀ مشتقی
تا مقدار بحرانی خویش کاهش یابد مجانب عمومی روی محور موهومی قرار می گیرد. مقدار بحرانی بهرۀ مشتقی ![]() بصورت زیر بدست می آید.
بصورت زیر بدست می آید.
(7-5) 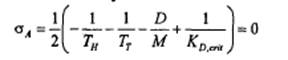
![]()
بنابراین پایداری سیستم تا زمانی که ![]() بیشتر از مقدار بحرانی خود انتخاب شود کاملاً
بیشتر از مقدار بحرانی خود انتخاب شود کاملاً
تضمین می شود[9 و 10].
حالتII: با وجود حلقه کنترلی انتگرالی
در این حالت تابع انتقال حلقه باز برای سیستم در شکل 3-5 به صورت زیر داده می شود.
(8-5) 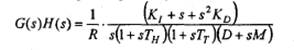
شکل 5-5 مکان هندسی ریشه های حاصل از (G(S(H(s را برای انواع مقادیر ![]() با استفاده از پارامترهای دیگر سیستم داده شده در جدول 1-5 را نشان می دهد.
با استفاده از پارامترهای دیگر سیستم داده شده در جدول 1-5 را نشان می دهد.
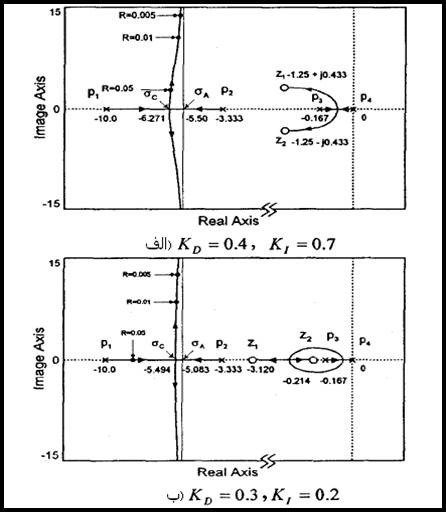
شکل 5-5: مکان هندسی ریشه هایبرای LFC بیشنهادی با حلقه انتگرالی
الف) ![]() ب)
ب) ![]()
مکان هندسی ریشه های شکل 5-5 با استفاده از ابزار مکان هندسی ریشه های MATLAB بدست آمد در این حالت حلقه های انتگرالی و مشتق پس خور، یک قطب و دو صفر به سیستم پس خور نسبی ساده اضافه کرده اند که از هر گونه حرکت سیستم به نیمه راست صفحۀ sممانعت به عمل می آورد.
همانطور که در حالت I مشاهده شد، رفتار سیستم حلقه بسته شدیداً به مقدار بهره مشتقی ![]() وابسته است و به محض کم تر شدن
وابسته است و به محض کم تر شدن ![]() ، مجانب عمودی به سمت راست حرکت کرد، این بدان معنی است که سیستم حلقه بسته می تواند ناپایدار باشد.
، مجانب عمودی به سمت راست حرکت کرد، این بدان معنی است که سیستم حلقه بسته می تواند ناپایدار باشد.
برای تضمین پایداریبه ازای هر مقدار مثبت R، بهره دیفرانسیلی ![]() باید از مقدار
باید از مقدار
بحرانی خود ![]() بزرگتر باشد.مقدار بحرانی بهرۀ مشتقی
بزرگتر باشد.مقدار بحرانی بهرۀ مشتقی ![]() را می توان به صورت زیر
را می توان به صورت زیر
محاسبه کرد.
(9-5) 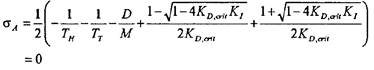
که مقدار ![]()
![]() به دست می آید.
به دست می آید.
همچنین باید توجه شود که رفتار پایداری سیستم حلقه بسته به بهرۀ انتگرالی ![]() نیز
نیز
بستگی دارد. برای بهره انتگرالی بالا مثل ![]() ، مکان هندسی ریشه هایممکن است ار نیمه راست صفحه s عبور کند (شکل 6-5) برای تضمین پایداری سیستم به ازای تمام مقادیر R بهره انتگرالی
، مکان هندسی ریشه هایممکن است ار نیمه راست صفحه s عبور کند (شکل 6-5) برای تضمین پایداری سیستم به ازای تمام مقادیر R بهره انتگرالی ![]() باید کمتر از مقدار بحرانی خود
باید کمتر از مقدار بحرانی خود ![]() انتخاب گردد. مقدار بحرانی بهره انتگرالی
انتخاب گردد. مقدار بحرانی بهره انتگرالی ![]() می تواند بوسیله ضابطۀ روث هورویتز به صورت زیر محاسبه شود.
می تواند بوسیله ضابطۀ روث هورویتز به صورت زیر محاسبه شود.
![]()
![]()
نتیجتاً، طرح LFC پیشنهاد شده شامل حلقه انتگرالی پس خور نیز پایداری سیستم را گارانتی می کند به شرط اینکه بهرۀ مشتقی ![]() از مقدار بحرانی خود
از مقدار بحرانی خود ![]() بیشتر و بهرۀ انتگرالی
بیشتر و بهرۀ انتگرالی ![]() از مقدار بحرانی خود
از مقدار بحرانی خود ![]() کمتر باشد.
کمتر باشد.
در اینجا بیان این نکته ضروری است که طرح کنترلی پیشنهاد شده می تواند اثرات میرایی را با استفاده از مشتق سیگنال فرکانسی به عنوانپس خور ورودی خود به خوبی بهبود بخشد.

شکل 6-5: مکان هندسی ریشه ها برای دو بهرهء انتگرالی ![]()
![]()
مدل سازی پیلوت هیدرولیکی با توجه به محدودیت های وضعیت سوپاپ
با سیاست نامنظم سازی، سیستم قدرت به احتمال زیادی در معرض اغتشاشات شدید قرار می گیرد که موجب می شود سیستم نوسان های زیاد و طولانی فرکانسی را متحمل شود. در چنین اختلال شدیدی سوپاپ بخار جهش های بزرگتری زیر حالتهای گذرا تجربه می کند. بنابراین لازم است محدودیت هایی برای موقعیت سوپاپ بخار در نظر گرفته شود.
جهت کنترل فرکانس بار اختلال های کوچک اهمیت زیادی دارند بنابراین باید به مدلسازی وضعیت سوپاپ بخار توجه شود.
در این بخش نشان داده شده می شود که راههای مختلفی برای مدلسازی موقعیت سوپاپ بخار وجود دارد و عملکرد کنترلی به صورت عمده ای به این مدلسازی در شرایط اختلال سیستم بستگی دارد. گاورنر هیدرولیک با محدودیت های وضعیت سوپاپ بخار به سه روش مدل سازی می شود (شکل7-5).
در مطالعات اولیه دو مدل اول بدست آمده اند. مدل سوم وقتی ممکن خواهد بود که یک پیستون نظیر آنچه در شکل7-5د نشان داده شده لحاظ می کنیم. دو مدل اولیه به نظر شبیه هم می آیند و ممکن است گمان شود که رفتار کنترلی شبیه هم داشته باشند.اما دریافته ایم که دو روش اولیه رفتارهای کنترلی کاملاً متفاوت با یکدیگر دارند[11].
در کنترل فرکانس بار اختلال های کوچک اهمیت زیادی دارند به همین دلیل مدلسازی وضعیت سوپاپ بخار بیشتر مورد توجه قرار می گیرد.

شکل 7-5 محدود کنندهء موقعیت شیر بخار
شکل 8-5 نوعی از پاسخهای کنترلی را برای سه حالت متفاوت با استفاده از سه مدل متفاوت نشان می دهد. در اینجا باید این نکته تذکر داده می شود که دو مدل اولیه به طور غافلگیر کننده ای نتایج یکسانی را بوجود آورده اند.
در اینجا هر سه مدل را با پارامترهای مختلف و اختلالات مختلف برای سیستم یک ماشینی امتحان شده است. از آنجایی که با مسئله کنترل بهینه حالت محدود مواجه هستیم که نیازمند کنترل حلقه باز می باشد، نتیجه گیری عمومی و کلی سخت به نظر می آید.

شکل 8-5 پاسخهایی از ω و xgv برای سه محدود کنندهء مختلف؛ الف) فرکانس ب) موقعیت دریچه.
به هر حال دریافته ایم که مدل محدود کننده بی پایان دستورالعمل کنترلی بهتری نسبت به آنهای دیگر برای تمامی حالت ها با توجه به، کنترل فرکانس بار ارائه می دهد. بنابراین از اولین مدل برای LFC استفاده خواهد شد.
روش پیگردی بهینه برای طرح LFC جدید
در این طرح از كنترل مشتقگیر بهره گرفته شده است و از آنجایی كه مشتق فركانس یك متغیر حالت نیست، لذا لازم است فرمولبندی جدیدی برای LFC ارائه كنیم تا بتوانیم كنترل بهینه را برای آن طراحی كنیم.
معادلات حالت را میتوان از شكل 3-5 بفرم زیر استخراج نمود:
| (10-5) | |
| (11-5) | |
| (12-5) | |
| (13-5) |
ورودی كنترلی را میتوان توسط سیگنالهای پس خور به فرم زیر نشان داد:
| (14-5) |
با جایگذاری رابطه (11-5) در (14-5) خواهیم داشت:
| (15-5) |
از رابطه بالا پیداست كه كنترل بهینه به اغتشاش بار بعنوان سیگنال فرمان نیازمند است.
می توان معادلات حالت مذكور را بصورت ماتریسی زیر در آورد:
| (16-5) | 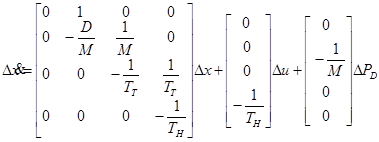 |
و
| (17-5) | 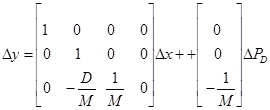 |
كه
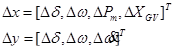 |
شاخص كارایی برای بهینهسازی كه باید حداقل شود بصورت زیر معرفی میشود:
| (18-5) |
با استفاده از شاخص بالا، مسئله LFC می تواند به فرم نرمال مسائل كنترل بهینه به صورت زیر نوشته شود:
| (19-5) | 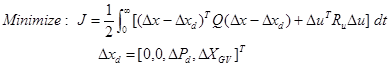 |
معادلات سیستم را نیز به شكل زیر بازنویسی میكنیم:
| (20-5) |
معادله ریكاتی و معادلات دیفرانسیلی برای s از تئوری كنترل بهینه بصورت زیر استخراج میشوند[9]:
| (21-5) | 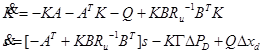 |
قانون كنترل بهینه با رابطه زیر تعیین می شود:
| (22-5) |
حالت ∆x را می توان با اندازهگیری ∆y و با بكارگیری عمل pseudo-inverse، تخمین زد:
| (23-5) |
با حل معادله ریكاتی و بكارگیری عمل pseudo-inverse، قانون كنترل بهینه بشكل زیر بدست میآید:
| (24-5) | 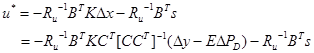 |
از آنجایی كه قانون كنترل بهینه توسط سیگنال پس خور ∆y نشان داده شده است، لذا بهرههای پس خور بهینه براحتی معین میشوند. بعلاوه سیگنال فرمان ![]() ، كه وابسته به اغتشاش میباشد، برای جبرانسازی اغتشاشات مورد نیاز میباشد.
، كه وابسته به اغتشاش میباشد، برای جبرانسازی اغتشاشات مورد نیاز میباشد.
بهبود توسعه تعدیل سیستم با استفاده از پس خور دیفرانسیلی در، کنترل فرکانس بار
پایداری سیستم قدرت اغلب وابسته به انرژی جنبشی اضافی ذخیره شده در ژنراتور دورۀ خطاست. کنترل شیر بخار مستقیم ترین روش برای کنترل انرژی جنبشی اضافی است. در اینجا طرح جدیدی از، کنترل فرکانس بار با استفاده از کنترل کننده اصلاح شده PID ارائه داده شده که تعدیل سیستم را بهبود می بخشد.
طرح جدید پشنهادی LFC از مدل بی پایان برای موقعیت شیر بخار استفاده می کند.
نشان خواهیم داد که کنترل سوپاپ بخار مستقیم ترین روش برای کنترل انرژی جنبشی اضافی ذخیره شده در ژنراتور در دورۀ خطا است و دستور العمل کنترلی شدیداً تحت تاثیر مدلسازی شیر بخار می باشد.
طرح کنترلی پیشنهاد شده برای دو سیستم ساده با 4 ماشین و 10 شین و سیستم 39 شین جدید انگلیسی بکار می رود.
با بزرگ تر و پیچیده تر شدن سیستم های قدرت مدرن خطر اینکه نوسان های سیستم در محیط های وسیع تری منتشر یابد بیشتر شده است.این قضیه انگیزۀ بسیاری از تلاشهای اخیرا برای توسه تکنیکهای پایداری سیستم برای تعدیل موثر انواع نوسان ها مانند نوسان های داخل منطقه ای طولانی مدت و نواسان های فرکانس پایین شده است.
پایدارای سیستم قدرت به انرژی جنبشی اضافی در ژنراتور در دوره خطا وابسته است انرژی اضافی بسته به دوام خطای سیستم کاملاً کوچک به حساب می آید. در بدترین و شدیدترین حالات انرژی اضافی تا 0.1( MWs pu) در ژنراتور شین خطا با عملکرد نرمال مدار شکن می رسد.
کنترل موثر انرژی جنبشی اضافی می تواند مستقیم ترین روش برای رسیدن به پایداری سیستم باشد و همینطور کنترل شیر بخار نیز مستقیم ترین روش برای کنترل انرژی جنبشی اضافی می باشد[12و13].
با استفاده از LFC خروجی مکانیکی در رنج [0.7~1.07]PU با توربیین فشار بالا می تواند کنترل شود که دارای پاسخ نسبتاً سریع تری از حلقه کنترلی Q-V می باشد. انرژی اضافی می تواند در 1 یا 2 ثانیه به طور کامل جذب شود به شرط اینکه گاورنر سرعت با برخی قوانین کنترلی بهینه مدار باز کنترل شود. چیزی که در عمل نمی توان به آن دست یافت.
به هر حال تجربه ثابت کرده است که LFC مرسوم به دلیل داشتن محدودیت های وضعیت سوپاپ بخار و رنج کنترلی محدود بهره های LFC پایداری سیستم را به خوبی نمی تواند فراهم کند.در عوض پایدار کننده سیستم PSS در رنج وسیعی برای تعدیل نوسان های سیستم از حلقه کنترلی Q-V برای کنترل قدرت خروجی ژنراتور استفاده می کند[14و15].
به هر حال PSS) Power System Stabilizer) دارای یک نقطه ضعف اساسی است و آن اینکه حلقه کنترلی Q-V دارای زمان پاسخ دهی طولانی است. در حالات اغتشاشات شدید نوسان های وسیع و طولانی مدت منجر به اثرات فرکانس قطع جریان بخار می شوند.
آنالیز کنترل انرژی اضافی
همانطور که گفتیم پایدارای سیستم شدیداً به انرژی جنبشی ذخیره شده در ژنراتور در دورۀ خطا بستگی دارد. بنابراین مستقیم ترین روش برای کنترل پایداری سیستم کنترل موثر این انرژی اضافی است.
انرژی جنبشی اضافی بادوام خطا به طور مناسبی افزایش می یابد. با فرض عملکرد نرمال مدارشکن ها، رله های حفاظتی قسمتی را که دچار خطا شده در 1. 0 ثانیه بعد از وقوع خطا از سیستم خارج می کنند. در شدیدترین حالات انرژی اضافی به 0.1 MWs در ژنراتور شین خطا می رسد. این انرژی تقریباً مقدار کاملاً کوچکی است که بوسیله دورۀ کنترلی 10 ثانیه ای بااستفاده از انواع ابزارهای ذخیره انرژی مانند SMES) Super-Conducting Magnetic Energy Storage) و ادوات FACTS به آسانی کنترل می شود.
در این راستا تلاش های بسیاری برای بهره برداری از این ابزارهای ذخیره انرژی برای پایداری سیستم به عمل آمده است. کاملا مشخص است که کنترل شیر بخار مستقیم ترین روش برای کنترل انرژی جنبشی اضافی است. با این حال توجه زیادی به استفاده از حلقه LFC برای پایدارای نشده است.
با تنظیم گاورنر سرعت در حلقه LFC، خروجی مکانیکی می تواند در رنج(0.7-1.07) PU با توربین فشار بالا کنترل شود که دارای عکس العمل سریعتری نسبت به حلقه کنترلی ولتاژ دارد.
کنترل انرژی اضافی با استفاده از اطلاعات جدول زیر تحلیل می شود.
جدول 2-5 اطلاعات برای توربین فشار بالا و حلقه LFC
| توربین فشار بالا | حلقه LFC |
| FTH=0.3[pu]
TCH=0.3 s |
TH=0.1 s
R= 5% |
TCH: ثابت زمانی توربین فشار بالا
TH: ثابت زمانی گاورنر سرعت
R: درصد تنظیم فرکلنس
اغلب ژنراتورهای گرمایی ظرفیت بالا از چرخه بازیافت دوباره گرما استفاده می کنند. توربین های فشار بالا %30 کل انرژی تولیدی را با ماکسیمم %125 قدرت نامی تولید می کنند. توربین بازیافت گرما دارای ثابت زمانی 10 تا 15 ثانیه می باشد. برای چندین ثانیه اول خطا، خروجی توربین بازیافت گرما ثابت می ماند. بنابراین رنج کنترلی خروجی ژنراتور (0.7-1.07) PU برای چندین ثانیه اول خواهد بود.
اگر انرژی اضافی در چند ثانیه بوسیله LFC با رنج کنترلی (0.7-1.07) PU جذب شود، انرژی اضافی تنها بوسیله LFC کنترل می شود آیا این امکان وجود دارد؟
برای پاسخ به این سوال ما باید کل زمان تاخیر را برای عکس العمل خروجی مربوط به کنترل امتحان کنیم. ثابت های زمانی مربوط به کنترل قدرت توربین فشار بالای LFC عبارتند از: ![]() و
و ![]() که در جدول 2-5 داده شده اند.زمان تاخیر برای عکس المل خروجی به صورت زیر داده می شود.
که در جدول 2-5 داده شده اند.زمان تاخیر برای عکس المل خروجی به صورت زیر داده می شود.
(25-5) ![]() برای محاسبه کل زمان مورد نیاز، فرض شده است قدرت تولیدی پست خطا 0.8pu مقدار قدرت نامی مجاز باشد.
برای محاسبه کل زمان مورد نیاز، فرض شده است قدرت تولیدی پست خطا 0.8pu مقدار قدرت نامی مجاز باشد.
از آنجا که رنج کنترلی قدرت بخار در محدودۀ (0.7-1.07) PU می باشد، کل زمان مورد نیاز برای جذب انرژی اضافی 0.1 PU به صورت زیر محاسبه می شود.
(26-5) T=Tdelay+ 0.1/0.1=1.4 s
در حالت های اختلالات شدید برای مثال، هنگام خطای پست که قدرت تولیدی به کمتر از 0.7PU کاهش می یابد، رنج کنترلی قدرت بخار با استفاده از قطع شیر کنترل می تواند کاهش یابد که بعداً در مورد آن بحث می شود.
محاسبات بالا با این پیش فرض انجام شده است که LFC یک کنترل بهینه را که فقط با کنترل حلقه باز غیر واقعی قابل دسترسی است فراهم می کند. از دیدگاه تئوری محاسبات بالا نشان می دهند که جذب انرژی اضافی در 2 ثانیه امکان پذیر است.
با این حال حلقه پاسخ دهی سریع LFC اغلب شامل نوسان است و تجربه ثابت کرده است که LFC معمول به علت رنج کنترلی محدود بهره های LFC و محدودیت موقعیت شیر بخار پایداری کمی در سیستم بوجود می آورد.
در عوض PSS معرفی شد و به طور وسیعی برای متعادلکردن نوسان های سیستم استفاده شد. PSS از حلقه کنترلی Q-V برای کنترل قدرت خروجی استفاده می کند بنابراین دارای یک نقطه ضعف اساسی بود و آن این بود که حلقه کنترلی Q-V دارای زمان پاسخ دهی طولانی بود.
PSS فرکانس و ولتاژ را به عنوان سیگنال های پس خور خود معرفی می کند. این سیگنال پس خوری مستقیماً به آمپلی فایر سیگنال AVR هدایت می شود.
حلقه کنترلی Q-V شامل ثابت های زمانی زیادی مانند زمانی سیم پیچی میدان ![]() و ثابت های زمانی محرک وابسته و ثابت های زمانی AVR وابسته می باشد. تمام ثابت های زمانی AVR وابسته در حد میلی ثانیه کوچک هستند و در محاسبات تاخیر پاسخ قابل صرف نظر کردن می باشد.
و ثابت های زمانی محرک وابسته و ثابت های زمانی AVR وابسته می باشد. تمام ثابت های زمانی AVR وابسته در حد میلی ثانیه کوچک هستند و در محاسبات تاخیر پاسخ قابل صرف نظر کردن می باشد.
ثابتهای زمانی مربوط به قسمت محرک نسبتا بزرگ و در حد 0.1sهستند. بزرگترین ثابت زمانی در حلقه کنترلی Q-V ثابت زمانی سیم پیچی میدان می باشد که در رنج زمانی7 تا 15 ثانیه می باشد، بنابراین تاخیر زمانی در کنترل Q-V معمولا بیشتر از 7 ثانیه است. پس کنترل PSS تاثیر کمی روی انرژی اضافی برای چند ثانیه بعد از خطا خواهد داشت.
در حقیقت می دانیم که اثرات کنترل PSS به سختی در چند ثانیه اول بعد از خطا مشاهده می شود.
با مقایسه تاخیر زمانی LFC با PSS به این نکته می رسید که حلقه LFC می تواند تعدیل سیستم را بهبود بخشد به شرطی که LFC برای غلبه بر مشکلات مرزهای محدود کنترل بهره های پس خور و محدودیت های موقعیت شیر، بهینه سازی شود.
توربین بدون باز گرمایش (Non – Reheat)
توربین نوع بدون باز گرمایش بوسیله فرمان تاخیر سیستم می تواند مدلسازی شود و کنترل کننده LFCپیشنهادی به صورت زیر در می آید.
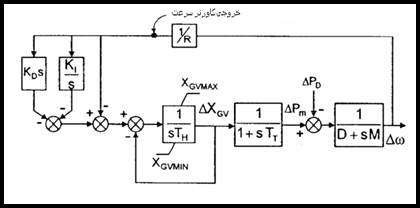
شکل 9-5 طرح کنترلی بیشنهاد شده برای توربین از نوع بدون باز گرمایش
دینامیک سیستم با استفاده از شکل بالا با تساوی زیر داده میشود:
(27-5)

برای اغتشاشات شدید با تحمل تغییرات فرکانسی، عکس العمل شیر بخار، فرا جهش بزرگتری را تحت حالت های گذرا تجربه می کند.
از آنجا که موقعیت شیر دارای محدودیت می باشد لازم است برای مطالعه پایدارای، این محدودیت در مدلسازی در نظر گرفته شود که نوعا در رنج o.40~1.20]pu] محدود می شود.
توربین با باز گرمایش
برای روشن شدن اثر طرح کنترل فرکانسی پیشنهاد شده به کار رفته توربین با باز گرمایش در شکل 10-5 نمایش داده شده است.

شکل10-5 بیکر بندی توربین نوع باز گرمایش

شکل11-5 طرح کنترلی بیشنهاد شده برای توربین از نوع باز گرمایش
جدول 2-5 مقادیر ثابت زمانی را نشان می دهد. فشار PT در شکل بالا مهمترین فشار بخار است که در طول مطالعه ثابت فرض شده است.
برای اغتشاشات شدیدتر و تغییرات وسیع فرکانسی، CV بوسیله کنترل کننده پیشنهادی در پاسخ به انحرافات فرکانسی موقعیت یابی می شود. محدودیت موقعیت CV مانند مدل بدون باز گرمایش بدست می آید.
اثرات دروپ (Droop) گاورنر، R
در طرح کنترلی معمول، افزایش بهره پس خور فرکانسی R ممکن است موجب ناپایداری سیستم شود. این حقیقت موجب می شود که رنج کنترل فرکانس اغلب روی %5 تنظیم شود.
با توجه به کنکاش هایی که در بخش هایی قبلی به عمل آمد به این نتیجه رسیدیم که سیستم کنترلی پیشنهاد شده بدون هیچ گونه محدودیتی در دروپ گاورنر پایداری سیستم را تضمین می کند. اثرات دروپ گاورنر روی فرکانس در شکل 12-5 مشاهده می شود که در آن پاسخ فرکانسی برای تغییرات %5 و %1 و %0.5 در R بدست آمده است. همینطور فرض شده است که سیستم تحت لغزش بار 200MW قرار داشته باشد.
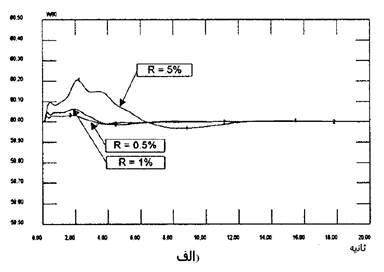
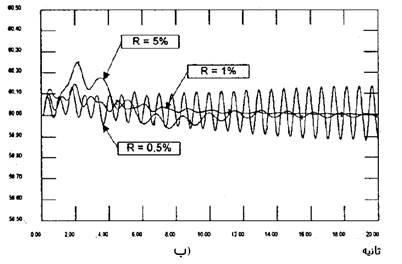
شکل 12-5 پاسخهای فرکانسی برای تنظیم سرعتهای مختلف R الف)کنترل کننده ارائه شده ب)کنترل کننده PI معمول
همانطور که در شکل 12-5 الف مشاهده می شود نوسانات فرکانس کنترلی شده با کنترل کننده پیشنهادی به محض اینکه دروپ گاورنر کاهش می یابد به سرعت تعدیل می شود. در حالی که کنترل کننده معمول دارای نوسانات فرکانسی طولانی و دراز مدت است) شکل 12-5 ب) برای کنترل کننده معمول سستی فرکانسی در حدR=0.5% ممکن است موجب شود قطب های سیستم به سمت راست صفحه S حرکت کنند.با این همه سیستم در حالت نوسانی باقی می ماند اما به حالت ناپایداری نمی رود زیرا محدودکننده وضعیت سوپاپ تعادل سیستم را نگه می دارد.
بررسی مشكل نویز
در این قسمت به انواع نویز های خواهیم پرداخت با PowerEn همراه باشید امیدوارم که تا اینجای کار خسته نشده باشید؛
كنترل سیستم بار فركانس با استفاده از پس خور نویزدار PID
این مقاله (شماره 9 و 10 مرجع) یك طرح كنترلی PID بر پایه پس خور متوسط گرفته شده ارائه می كند تا یك سیستم كنترلی با دیفرانسیل نویزدار با كاربرد آن بر كنترل بار فركانس در سیستم های قدرت تحقق یابد. مشخص است كه LFC در محیط های نویزدار قرار می گیرد. محیط نویزدار موجب می شود تا اتخاذ یك حلقه پس خور دیفرانسیلی مشكل باشد، چون مشتقات سیگنال در اثر نویزهای بار فركانس بالا بدتر می شوند و باعث ناپایداری سیستم می گردند[9و10].
این مقاله، یك طرح جدید كنترلی PID بر پایه مشتقات متوسط سیگنال به عنوان یك سیگنال پس خور دیفرانسیلی مبنی بر نادیده گرفتن اثرات نویزهای فركانس بالا ارائه می كند. این مطالعه، یك كاربرد پس خور دیفرانسیلی متوسط را در مورد LFC در سیستم های قدرت را بررسی می كند. طرح كنترلی ارائه شده، برای كنترل بار فركانس سیستم های قدرت تست شده است.
كنترل ID یكی از پركاربردترین روش های كنترل در زمینه های مختلف تقریباَ همه صنایع از جمله كنترل فرآیند شیمیایی وضعیت مكانیكی و یا كنترل سرعت به خا طر سادگی آن در اجرا می باشد.
در صنعت سیستم قدرت، واضح است كه كنترل بار فركانس در معرض محیط نویزی قرار می گیرد. دلیل آن سوئیچینگ های on/off بسیار زیادی است كه در طرف بار صورت می گیرد و نویز قابل توجهی را در اندازه گیری فركانس تولید می كند.
مشتقات سیگنال ها خیلی سریع تراز آنی تغییر می كنند كه وسایل كنترلی بتوانند از آن ها پیروی كنند و یا خروجی مشتق گیر، مقادیر بسیار بالایی تولید می كند كه سیگنال پس خور باید برای بیشتر فاصله های زمانی بریده شود، كه باعث می شود به دست آوردن اثرات كنترل دیفرانسیلی تقریباَ غیرممكن گردد. بنابراین اخیراَ، به استفاده از PI نسبت به كنترل PID در محیط های نویزی گرایش پیدا شده است.
از طرف دیگر واضح است كه اگر مشكل نویز تا حدی حل شود PID كارایی بیشتری از كنترل PI خواهد داشت. تلاشهای زیادی برای استفاده از فیلتر در حلقه پس خور دیفرانسیلی برای كاهش نویز انجام داده اند. یك فیلتر پایین گذر میتواند به حلقه پس خور دیفرانسیلی به صورت سری اضافه شود تا مشكل نویز را حل كند. اگر چه، مسائل دیگری را در پس خواهد داشت:
1) اكر تابع فیلتر تقویت شود اثرات پس خور سیگنال دیفرانسیلی كاهش می یابد.
2) اضافه شدن بلوك فیلترینگ، رفتار سیستم را تغییر می دهد و ممكن است هنگامی كه ورودی پس خور افزایش می یابد، موجب ناپایداری گردد.
در محیط های نویزدار، باید نوع جدیدی از کنترل کننده PID طراحی شود تا نویز قابل تحمل تر باشد. به منظور حل این مشكل كه مشتق گیرها، نویزهای فركانس بالا را تقویت می كنند، این مقاله، طرح جدید PID را ارائه می كند كه در آن مشتقات سیگنال به عنوان سیگنال پس خور دیفرانسیلی اتخاذ شده اند. مشتق متوسط به آسانی با استفاده از یك عامل تأخیر، به دست می آید و با تأخیرات زمانی به اندازه كافی كوچك، ما می توانیم مشتق متوسطی را به دست آوریم كه به مشتقی كه از حذف اثرات نویز به دست می آمد، نزدیك باشد. در اینجا باید این نكته یادآوری گردد كه زمان تأخیر نباید از كوچكترین ثابت زمانی سیستم بیشتر باشد چون T بزرگ، موجب تأخیر بیش از حد در پس خور دیفرانسیلی می گردد.
این مطالعه، به یك كاربرد پس خور دیفرانسیلی در مورد LFCدر سیستم های قدرت مرتبط می باشد. به دلیل سوئیچینگ های غیر قابل شمارش در سمت كاربران، اندازه گیریهای فركانس سیستم معمولاَ به خاطر نویز سخت تر می شود. در این محیط های نویزی، معمولاَ مهندسین PI را به PID ترجیح می دهند. در این مطالعه، ما خروجی های سه رویه مختلف را مقایسه می كنیم:
1) طرح كنترلی PID با صرف نظر از اثرات نویز
2) طرح كنترلی PTO كه از مشتقات متوسط استفاده می كند.
3) طرح كنترلی دیفرانسیلی فیلتر شده معمول كه از جایگزینی بلوك دیفرانسیلی به وسیله یك مشتق گیر به اضافه یك فیلتر درجه اول حاصل می شود.
اغتشاشات سیستم، یك پله واحد در نظر گرفته شده اند. سیستم ارائه شده برای چندین سیستم ساده با استفاده از بهره های پس خور مختلف آزمایش شده است. كنترل PID ارائه شده عملكرد بسیار خوبی شبیه به پاسخ سیستم اصلی با در نظر گرفتن نویز ارائه می كند.
دلیل نویز های کنترل فرکانس بار سوئیچینگ های on/off بسیار زیاد در شبکه می باشد و مشکل دیگر حضور این کلیدزنی در سمت مشتری می باشد که قابل کنترل نیست
آنالیز حلقه پس خور دیفرانسیلی معمول با در نظر گرفتن یك فیلترینگ
كنترل PID معمول، نواقص زیادی در محیط های نویزی دارد، چون مشتق گیر نویزهای فركانس بالا را تقویت می كند و این ممكن است فشار زیادی بر روی سیستم اعمال كند و تأثیرات بدی بر روی عملكرد کنترل کننده خواهد داشت. نتیجتاَ، بیشتر طرح های كنترلی PID، فیلترینگ را در نظر می گیرند. یك نمونه از طرح كنترلی PID كه فیلترینگ را در نظر گرفته، در شكل 13-5 نشان داده شده است[11].
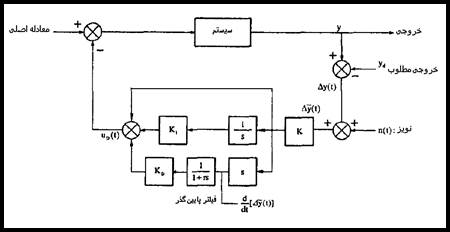
شکل 13-5 بلوک دیاگرام کنترل کننده PI عمومی
در سیگنال پس خور PID كه شامل نویزمی باشد، نویز به شدت به وسیله بخش مشتق گیر، تقویت می شود. ورودی و خروجی بخش مشتق گیر در شكل 14-5 نشان داده شده است.

شکل 14-5 سیگنال ورودی و خروجی کنترل کننده مشتق گیر
به خاطر تضمین حداقل تغییرات در رفتار سیستم بسته به بلوك الحاقی، معمولاَ در بیشتر موارد یك فیلتر پایین گذر در نظر گرفته می شود.
ما در اینجا، یك حلقه پس خور دیفرانسیلی در نظر می گیریم. تابع تبدیل كل شامل فیلتر به صورت زیر داده شده است.
(28-5) 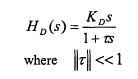
تابع تبدیل یابی، می تواند به صورت زیر نوشته شود:
(29-5) 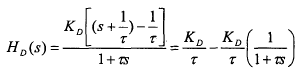
به خاطر كم كردن اثرات فیلتر، ثابت زمانی آن باید كوچك انتخاب شود. چون خیلی كوچك بودن t، ممكن است منجر به فیلترینگ ناقص شود، ثابت زمانی t را معمولاَ، چندین برابر دوره نویز با كمترین فركانس در نظر می گیرند. تصاویر فیزیكی در حوزه زمان ![]() و پاسخ ضربه آن متناظر با
و پاسخ ضربه آن متناظر با ![]() می باشد. پاسخ ضربه
می باشد. پاسخ ضربه ![]() به صورت زیر داده شده است:
به صورت زیر داده شده است:
(30-5) ![]()
که در آن ![]() تابع دلتای دیراک و
تابع دلتای دیراک و ![]() تابع پله واحد می باشند و سیگنال پس خور دیفرانسیلی
تابع پله واحد می باشند و سیگنال پس خور دیفرانسیلی ![]() به وسیله انتگرال كانولوشن زیر داده شده است:
به وسیله انتگرال كانولوشن زیر داده شده است:
(31-5) 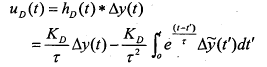
که در آن:
(32-5) ![]()
پس خور دیفرانسیلی با یك فیلتر درجه اول از جمع دو سیگنال به دست می آید: اولی یك سیگنال نسبی است و دیگری، انتگرال خطا با عامل ![]() می باشد. بنابراین، پس خور دیفرانسیلی معمول، ممكن است كنترلی دیفرانسیل موفقی را به دست نیاورد.
می باشد. بنابراین، پس خور دیفرانسیلی معمول، ممكن است كنترلی دیفرانسیل موفقی را به دست نیاورد.
طرح PID جدید با استفاده از تأخیر
در محیط نویزدار، لازم است یك نوع جدیدی از کنترل کننده PID را طراحی كنیم تا نویر تأثیری نداشته باشد. به خاطر حل این مشكل كه مشتق گیر، نویزهای فركانس بالا را تقویت می كند، این مقاله، یك طرح جدید PID ارائه می كند كه مشتق های متوسط سیگنال را به عنوان سیگنال پس خور دیفرانسیلی در نظر گرفته است تا اثرات نویزهای فركانس بالا را از بین ببرد. مشتقات متوسط به آسانی با استفاده از عناصر تأخیر به صورت زیر به دست می آید:
(33-5) 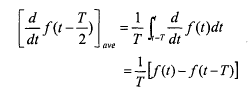
تبدیل لاپلاس مشتق متوسط به صورت زیر است:
(34-5) 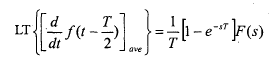
مشتق متوسط به آسانی با استفاده از تأخیر به دست می آید:
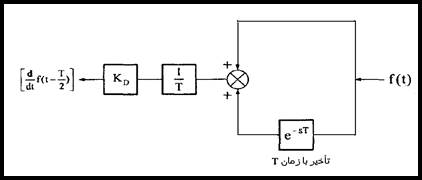
شکل 15-5 بلوک دیاگرام پس خور مشتق های متوسط سیگنال
اگر T را به اندازه ی كافی كوچك فرض كنیم، می توانیم مشتق متوسط را نزدیك به مشتق ناشی از بین رفتن اثرات نویز به دست آوریم. باید یادآوری شود كه تأخیر زمانی T نباید از كوچكترین ثابت زمانی تجاوز کند، چون ثابت زمانی بزرگ، موجب تأخیر زیادی در پس خور دیفرانسیلی می گردد.
بهتر است كه دو تابع تبدیل را برای حلقه دیفرانسیلی یكی برای کنترل کننده PID ارائه شده و دیگری برای کنترل کننده PID فیلتر شده معمول مقایسه كنیم.
(35-5) 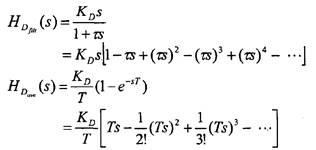
هر دو تابع تبدیل وقتی ![]() ، به
، به ![]() نزدیك هستند..
نزدیك هستند..
این نشان می دهد كه می دهد كه طرح كنترلی PID ارائه شده، مشكل را تا حدودی حل می كند و اضافه كردن بلوك فیلترینگ كه با كنترل بهرهء پس خور همراه است، رفتار سیستم را خصوصاَ در پابداری سیستم تغییر می دهد.
كاربردها
در كاربردهای عملی، مشكل LFC (كنترل بار فركانس) را در سیستم های قدرت در نظر می گیریم. بسته به سوئیچینگ های on-off غیر قابل شمارشی كه در سمت مشتریان انجام می گیرد، فركانس سیستم به دلیل نویز، بدتر می شود. معمولاَ مهندسین ترجیح می دهند كه در محیط های نویزی از PI به جای PID استفاده كنند. اگرچه، كاربرد كنترل PID برای LFC نشان می دهد كه بیشترموارد پیشرفته سیستم تأمین می شود. یك نمایش بلوکی همانطور كه در شكل 16-5 نشان داده شده است[9و10].
حلقه پس خور دیفرانسیلی آن دارای یك مشتق گیر ساده است، می تواند سیستم LFC را نشان دهد. با صرف نظر از اثرات نویز، ما می توند آنالیز پایداری سیستم را با آزمایش مکان هندسی ریشه های سیستم انجام دهیم. شکل 17-5، مكان هندسی را با افزایش بهره ورودی k نشان می دهد.

شکل 16-5 بلوک دیاگرام سیستم
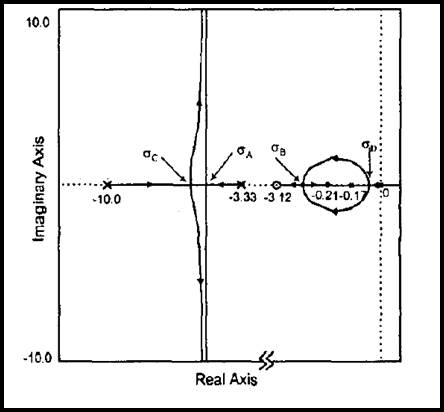
شکل 17-5 مکان هندسی ریشه های سیستم
به آسانی از مکان هندسی ریشه های بالا نتیجه گیری می شود كه سیستم داده شده در تمامی رنج های كنترلی بهره ی پس خور k پایدار می باشد به شرطی كه نویز سیستم، قابل صرف نظرکردن باشد. در محیط های نویزدار، حلقهءپس خور دیفرانسیلی باید به وسیله حلقه دیفرانسیلی فیلتر شده یا حلقه پس خور مشتق ارائه شده با تأخیر، جایگزین شود. شکل 18-5، طرح كنترلی PID ارائه شده را با استفاده از تأخیر نشان می دهد.
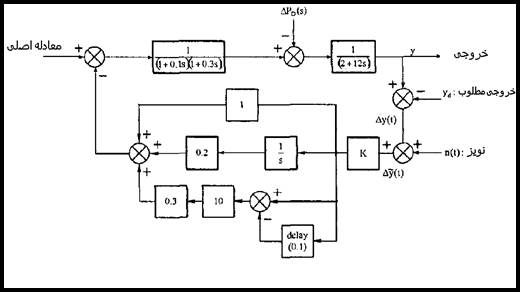
شکل 18-5 طرح کنترلی بیشنهادی با عناصر تاخیر
در سیستم بالا، زمانی تأخیر T، 0.1 ثانیه انتخاب شده است.
در این مطالعه، خروجی های سه سیستم مختلف را مقایسه می كنیم:
- طرح كنترلی PID بدون در نظر گرفتن اثرات نویز همانطور كه در شكل 4 نشان داده شده است.
- طرح كنترلی PID ارائه شده همانطور كه درشکل 18-5 نشان داده شده است.
- طرح كنترلی PID دیفرانسیلی فیلتر شده معمول با 0.1 =
 ، همانطور كه در شكل 5 – 13 نشان داده شده است.
، همانطور كه در شكل 5 – 13 نشان داده شده است.
اغتشاش سیستم، یك پله واحد در نظر گرفته شده است.
سیستم ارائه شده، برای بهره های پس خور k آزمایش شده است. خروجی ها، با دو طرح كنترلی دیگر مقایسه می شوند. عملكرد سیستم با تنظیم بهرهءپس خور K از 10 تا 300 آزمایش می شود. انحرافات فركانس در شكل 19-5 نشان داده شده است.
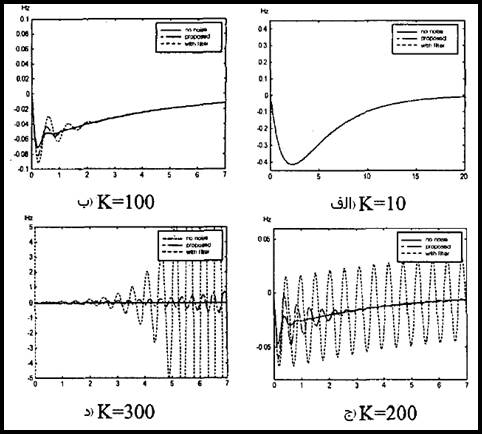

شکل 19-5 مقایسه خروجی های سه سیستم
در مورد 100= k همانطور كه در شكل 19-5الف نشان داده شده است. اگرچه پاسخ سیستم زیاد سریع نیست. هر سه طرح كنترلی PID، تقریباَ نتایج یكسانی را تولید می كنند.
در مورد 100= k نتایج شبیه سازی در شكل 19-5ب نشان داده شده است كه مشخص می كند كه طرح كنترلی ارائه شده، نتایج بسیار بهتری را از كنترل PID فیلتر شده معمول به دست می دهد. همچنین پاسخ سیستم، بسیار سریعتر از پاسخ های سیستم در 10= k است.
همچنین باید یادآوری شود كه کنترل کننده ارائه شده، خروجی های بسیار نزدیكتری به خروجی های كنترل PID بدون در نظر گرفتن نویز دارد. این نشان می دهد كه كنترل بدون نویز با استفاده از كنترل PID ارائه شده با تأخیر به دست می آید.
شكل 19-5 ج نشان می دهد كه وقتی فیلتر به مشتق گیر اضافه می شود، همانطور كه قبلاَ گفته شده بود رفتارهای سیستم با افزایش k تغییر می كند. همچنین طرح كنترلی ارائه شده، رفتارهای سیستم را خیلی كمتر تغییر می دهد و سیستم در شرایط پایدار باقی می ماند.
در مورد k=300، هر دو طرح كنترلی ارائه شده و فیلتر شده معمول، سیستم را به خاطر بهرۀ پس خور بالا ناپایدار می كنند به عبارت دیگر، اثبات می شود كه كنترل اصلی، سیستم را وقتی از اثرات نویز صرف نظر كنیم بدون توجه به بهره k پایدار نگه دارد كه قبلاَ با استفاده از مکان هندسی ریشه های توضیح داده شد.
شكل 20-5 خروجی های مدارت مشتق گیر، خروجی مشتق گیر، خروجی فیلتر شده آن و خروجی مشتق متوسط را نشان می دهد. مشاهده می شود كه هر دو سیستم متوسط و مشتق فیلتر شده به طور مساوی نویز خروجی الف مشتق گیر را فیلتر می كنند و سیگنال یكسانی حاصل می كنند.
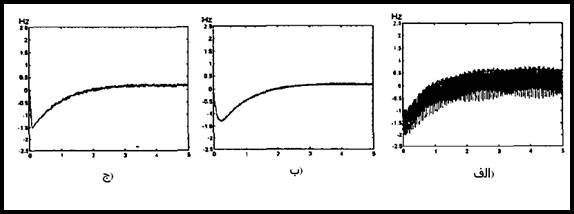
الف) خروجی دیفرانسیلی همراه نویز ب) مشتق گیر فیلتر شده ج) مشتق متوسط شده
شكل 20-5 خروجیهای مدارهای دیفرانسیلی با k=10
نتایج شبیه سازی
طرح کنترلی پیشنهاد شده با پارامترهای گوناگون و ناپایداری های گوناگون برای سیستم تک ماشینی امتحان شده است. برای حالت ناپایداری فرض شده است که سیستم تحت تغییرات پله ای بار 0.4pu قرار داشته باشد.
نتایج شبیه سازی ω در شکل 21-5 نشان داده شده است.
شكل 21-5 پاسخهایی از ω برای تغییرات بار پله ای 0.4 pu
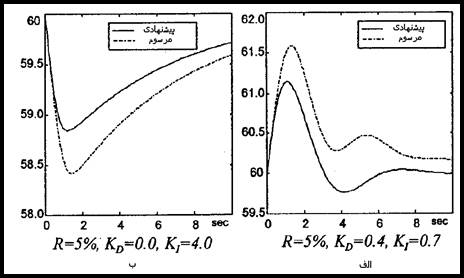
برای هر نوع تغییرات بار، کنترل کننده پیشنهادی کنترل بهتری را از نوع معمول آن دارد. تأثیر تنظیم سرعت R روی هر کنترل کننده را در شكل 22-5 می توانید مشاهده کنید.
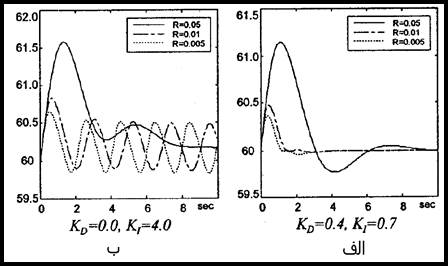
شكل 22-5 پاسخهایی از ω برای تنظیم سرعت R های مختلف.
الف) کنترل کننده پیشنهادی ب) کنترل کننده معمول
چیزی که اینجا قابل توجه است این است که کنترل کننده پیشنهادی برای اختلال های بزرگ به تنظیم سرعت حساس نیست.
تحلیل های دیگر در LFC محدودیت سرعت سوپاپ زنی و تحلیل سرعت تولید(GRC) می باشد. حد سرعت سوپاپ زنی GRC به ترتیب1.5pu/sec، 0.20pu/sec فرض می شوند یعنی:
(36-5) ![]()
پاسخهای کنترلی سیستم با این تحلیل در شکل 23-5 داده شده اند. در محدودیت سرعت سوپاپ زنی و GRC کنترل کننده پیشنهادی عملکرد خوبی خواهد داشت در حالی که کنترل کننده معمول دارای پاسخهای نوسانی است.
باید به این نکته توجه بشود که کنترل کننده پیشنهادی دارای مقدار کمی نوسان در هنگام کاهش تنظیم سرعت می باشد.
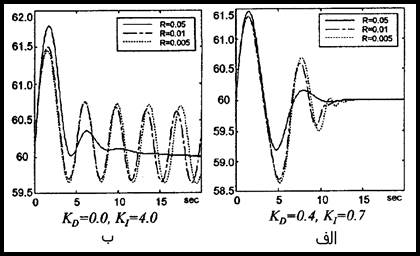
شكل22-5 پاسخهایی از ω و xgv تحت GRC الف) کنترل کننده پیشنهادی ب) کنترل کننده معمول
طرح كنترل بهینه پیشنهادی برای یك سیستم تك ماشینه مورد آزمایش قرار گرفته است. اغتشاش بار بصورت پلهای و به اندازه 0.4pu در نظر گرفته شده است. پارامترهای سیستم نیز در جدول 1-5 ذكر شدهاند.
با استفاده از این پارامترها، معادله ریكاتی و معادلات دیفرانسیلی سیگنال فرمان نتایج بهینه زیر را ارائه می کند.
| (37-5) | 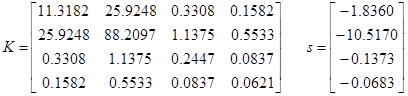 |
با حل معادله ریكاتی، میتوان بهرههای پس خور بهینه و سیگنال فرمان را بدست آورد:
| (38-5) | 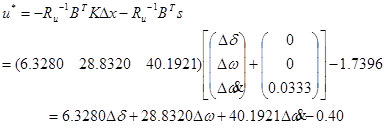 |
با نرمالیزه كردن رابطه بالا نسبت به ضریب ∆ω میتوان بهرههای كنترل بهینه و ضریب تنظیم سرعت را بدست آورد.
| (39-5) | 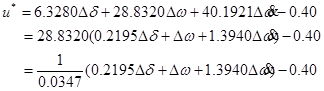 |
یادآوری میشود كه سیگنال فرمان در اینجا برابر اغتشاش 0.4pu میباشد.
بهره های پس خور بهینه و نیز بهرههای پس خور PID نمونه در جدول زیر آورده شدهاند. نتایج شبیهسازی برای بار پلهای افزایش یابنده در شكل 23-5 نشان داده شدهاند.
جدول 3-5: بهرههای پس خور برای هر یك از كنترلكنندهها
| کنترل کننده
بهره |
کنترل کننده پیشنهادی | کنترل کننده معمول | |
| بهینه | سعی و خطا | ||
| تنظیم سرعتR | 0.0347 | 0.05 | 0.05 |
| انتگرالی Kl | 0.2195 | 0.7 | 4.0 |
| دیفرانسیلی Kd | 1.3940 | 0.4 | 0.0 |
واضح است كه کنترل کننده پیشنهادی با بهرههای پس خور بهینه، عملكرد كنترلی بهتری دارد نسبت به حالتی كه این ضرایب بصورت سعی و خطا انتخاب شدهباشند.
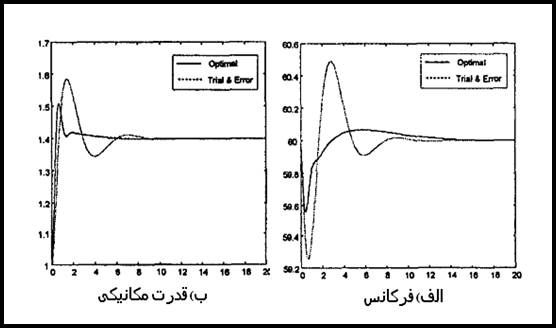
شكل 23-5: منحنی پاسخ ω و Pm برای بار افزایشی 0.4pu
کنترل کننده پیشنهادی دارای مقدار کمی نوسان در هنگام کاهش تنظیم سرعت می باشد
ورودی كنترلی و شاخص كارایی در شكل 24-5 نمایش داده شدهاند. زمانی كه ورودی كنترلی بهینه مورد استفاده قرار گیرد، سیستم، فراجهش بزرگتری خواهد داشت كه در عین حال در عرض چند ثانیه میرا میشود.
همان طور كه از شكل 24-5 ب پیداست، شاخص كارایی سیستم با کنترل کننده بهینه كوچكتر از موردی است كه از سعی و خطا استفاده شدهاست.

شكل 24-5: منحنی پاسخ ورودی كنترلی و شاخص كاركرد
تحت اغتشاشات بزرگ، پاسخ شیر بخار، فرا جهش های بزرگی را در شرایط زیرگذرا تجربه میكند. در عمل برای جریان بخار یك محدودیت ماكزیمم وجود دارد. برای لحاظ كردن تأثیر محدودیت موقعیت شیر بخار در كنترل بهینه، این محدودیت را در رنج [0.4~1.2] p.u. در نظر میگیریم. نتایج این شبیه سازی در شكل زیر آمدهاست.
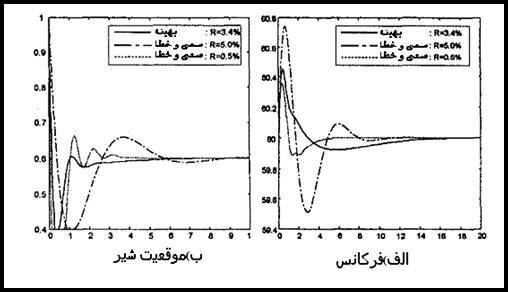
شكل 25-5: منحنی پاسخ فركانس و موقعیت شیر به مقادیر متفاوت ضریب R
اثر فرکانس قطع موقعیت شیر باعث ایجاد یك محدودیت از طرف پایین برای موقعیت شیر بخار میگردد كه در اینجا این محدودیت پایین 0.4pu میباشد.
با توجه به مباحث ارائه شده میتوان چنین گفت كه کنترل کننده طراحی شده با استفاده از روشهای بهینه دارای عملكرد بهتری نسبت به سایر طرحهای کنترل فرکانس بار میباشد. همچنین با استفاده از تكنیك فیلترینگ ارائه شده در اینجا می توان به نحو مطلوبی تأثیر نویزهای فركانس بالا را از بین برد.
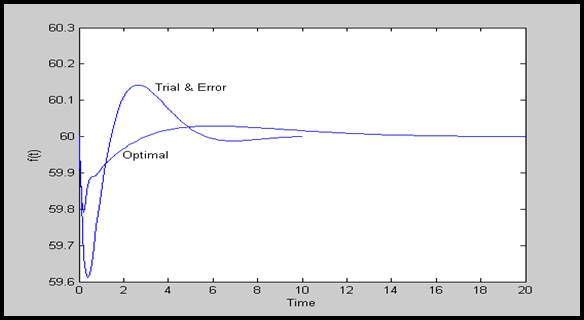
شکل 26-5: پاسخ (f(t برای سیستمهای با بهرههای بهینه و بهرههای بدست آمده از سعی و خطا
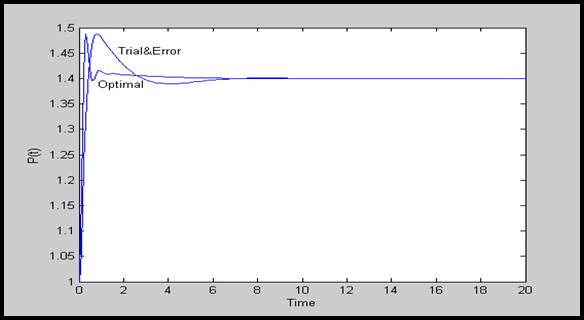
شکل27-5: پاسخ (Pm(t برای سیستمهای با بهرههای بهینه و بهرههای بدست آمده از سعی و خطا
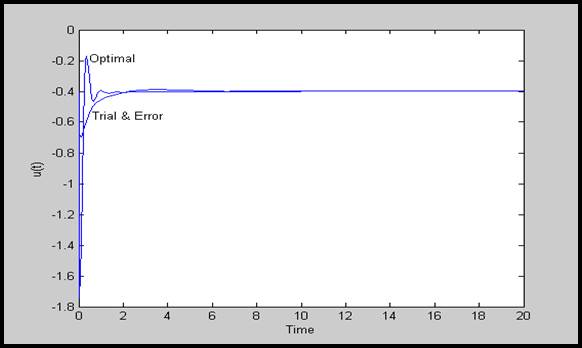
شکل 28-5: پاسخ (u(t ورودی كنترلی برای سیستمهای با بهرههای بهینه و بهرههای بدست آمده از سعی و خطا
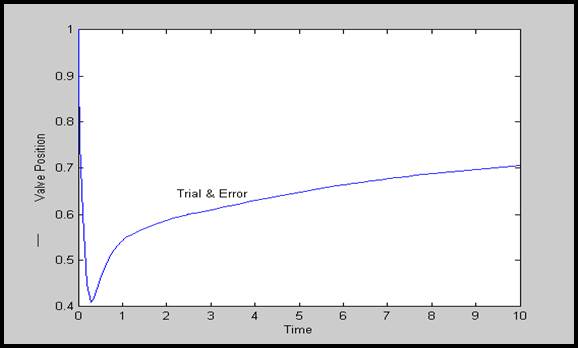
شکل 29-5: تغییر موقعیت شیر بخار برای سیستم با بهرههای بدست آمده از سعی و خطا
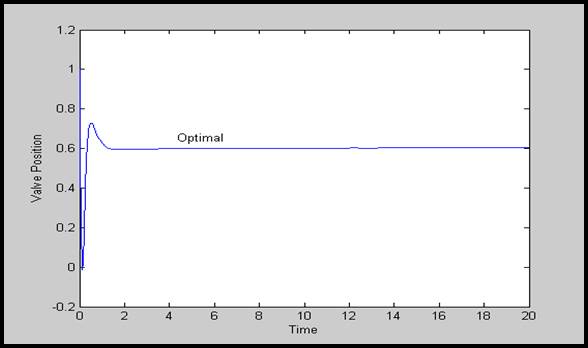
شکل 30-5: تغییر موقعیت شیر بخار برای سیستم با بهرههای بهینه
کاربرد در سیستم قدرت
از آنجایی که کنترل کننده پیشنهادی در بخش های قبلی با استفاد از مکان هندسی ریشه های تحلیل گردید، بسیار مهم است که، کنترل فرکانس بار پیشنهادی برای سیستم قدرت غیر خطی واقعی آزمایش شود.
سیستم قدرت با 4 ماشین و 10 باس
شبیه سازی کامپیوتر برای سیستم با 4 ماشین و 10 شین انجام شد. تمام شبیه سازی ها بروی پکیج CYME انجام شد که یک برنامه پایداری گذرای غیر خطی می باشد. پیکربندی سیستم در شكل31-5 نمایش داده شده است.

شكل 31-5 سیستم با 4 ماشین و 10 شین
ژنراتور شماره 1 بوسیله تحریک dc و سایر ادوات بوسیله متحرک های تریستوری با بهره انتقالی بالا تحریک می شوند. فرض شده است که فقط ژنراتور شماره 4 به طرح کنترلی پیشنهاد شده مجهز شده است.
برای حالت اغتشاشات زیاد، فرض شده است که تغییرات پله ای بار در شین 8 به اندازه 200mw باشد[8].
سیستم قدرت مورد مطالعه بوسیلۀ نوسان های فرکانس پائین حدود 0.2Hz تحت آسیب قرار می گیرد شکل 32-5 نشان دهندۀ پاسخ فرکانسی ژنراتور شماره 4 برای تغییرات بار می باشد.

شکل 32-5 پاسخهایی از ω برای لغزش بار MW200
کاملاً مشخص است که طرح کنترلی پیشنهاد شده عملکرد کنترلی قابل توجه و عالی را در مقایسه با کنترل کننده PI معمول داراست.
سیستم جدید انگلیسی با 10 ماشین و 39 شین
طرح کنترلی بیشنهاد شده برای سیستم انگلیسی با 39 شین امتحان شده است که ژنراتورهای آن با دو مدل طراحی شده اند. ژنراتورها به جز شماره 1 با محرک منعکس کنندهء اثر اشباع نوع یک IEEE مجهز شده اند.
خطای سه فاز در شین شماره 6 با دوام 0.1 sec بعنوان اغتشاش سیستم لحاظ شده است. این خطای سه فاز سبب وقوع مدل ساده ای از ناپایداری ژنراتور نزدیک نقطه خطا می شود که به نوبه خود موجب از بین رفتن سنکرونیزم در قسمتهای دیگر سیستم می گردد.
ژنراتور شماره 2، 3، 7، 1 و 9 نزدیک نقطه خطا به کنترل کننده فرکانسی پیشنهادی مجهز شده اند. شکل زیر نشان دهندهء فرکانس و قدرت الکتریکی ژنراتور 2 و مقایسه با کنترل کننده PI معمول می باشد.
از این مقایسه به آسانی در می یابید که کنترل کننده پیشنهاد شده بصورت کاملا مشخصی تعدیل سیستم را بهبود می بخشد.
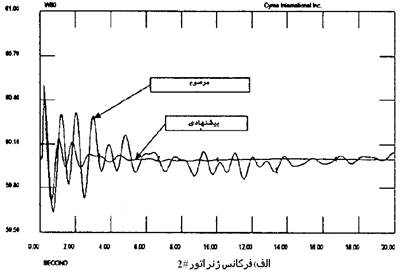

![]()
شکل 33-5 پاسخ های فرکانسی و قدرت الکتریکی کنترل کننده پیشنهاد شده و مقایسه با کنترل کننده PI معمول.
اثر دروپ گاورنر بوسیله شکل 34-5 مشخص شده است جایی که پاسخ های فرکانسی با تنظیم R روی 5%، 0.1% و 0.5% بدست آمده اند. همانطور که در شکل دیده می شود کنترل کننده پیشنهاد شده تعادل سیستم را افزایش و دروپ گاورنر را کاهش می دهد.
بنابراین LFC بیشنهاد شده می تواند به عنوان یک ابزار قدرتمند برای بهبود تعدیل سیستم بجای PSS معمول به کار رود.
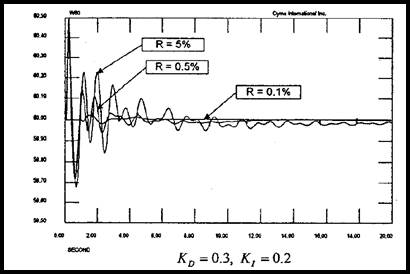
شکل 34-5 پاسخهای فرکانسی برای دروپ های مختلف گاورنر.
نتیجه گیری
در این پست تخصصی ابتدا با استفاده از فرضیات مناسب مدل سیستم بار – فرکانس با یک ژنراتور ارائه شد و نحوه ی کنترل آن مورد بررسی قرار گرفت. سپس با تعریف نواحی کنترل، مدل ارائه شده برای یک ژنراتور به مدل بار- فرکانس نواحی قدرت بسط داده شد و اهداف کنترل خودکار تولید مطالعه گردید و در نهایت با توجه به اینکه جهت اعمال کلیه روش های کنترل مدرن، به معادلات حالت سیستم نیاز می باشد، معادلات مذکور با استفاده از مدل به دست آمده در قسمت های قبل ارائه شد.
البته کلیه معادلات حوزه فرکانس و معادلات حالت سیستم با بهره گیری از تقریب های مقرون به صحت به صورت خطی بیان گشته اند. عوامل غیر خطی موجود در سیستم به شکل عناصر جداگانه ای بررسی شده اند و می توانند به مدل کلی سیستم اعمال شوند.
به خاطر غلبه كردن بر نواقص كنترل PIDمعمول، برخی مقالات پس خور مشتقات متوسط را در محیط های نویزی معرفی می كنند و یك كنترل کننده PID جدید با تأخیر را توصیه می كند تا كنترل دیفرانسیلی به دست آوریم كه نویز را تحمل كند.
همچنین طرح جدیدی از LFC با کنترل کننده PIDاصلاح یافته ارائه شده است که پایداری حلقه LFC را برای رنج های وسیعی از بهره های پس خور PID تضمین می کند. طرح کنترلی معمول PID دارای این مشکل بود که افزایش هر کدام از بهره های PID موجب ناپایداری حلقه LFC می شد.
با مشاهده این واقعیت که نسبت بین بهره های پس خور PID دارای اطلاعات بیشتری از تک تک بهره های پس خور PID است، کنترل کننده اصلاح یافته PID پیشنهاد شد. کنترل کننده اصلاح یافته PID دارای مدارهای پس خور دیفرانسیلی و انتگرالی با استفاده از خروجی گاورنر سرعت گوی چرخان می باشد. همچنین نشان داده شد که عملکرد کنترلی به شدت به مدل سازی سوپاپ بخار در حالت های اختلالات شدید سیستم وابسته است.
نتایج شبیه سازی نشان دادند که با استفاده از طرح کنترلی پیشنهاد شده عملکرد کنترلی به صورت خارق العاده ای بهبود می یابد
پیشنهادات
- وضع قوانین تجاری مناسب جهت ایجاد رقابت سالم در بازار LFC
- تعیین معیارهای استاندارد جهت قیمت گذاری LFC و دیگر سرویس های جانبی
- استفادهاز لینک های مخابراتی جهت مانیتورینگ و مشاهده اطلاعات مربوط به بازار به صورت on-Line
- طراحی نرم افزارهای حسابداری مناسب جهت چگونگی دریافت و پرداخت هزینه
- تهیه بانک های اطلاعاتی در خصوصی منابع LFC مورد استفاده توسط هر شرکت
- استفاده از روشهای بهینه سازی براساس پایداری و شرایط اقتصادی در تعیین پارامترهای کنترل کننده فرکانس
منابع
[1] حیدر علی شایانفرو شهرام جدید و احد کاظمی، بررسی سیستم های قدرت جلددوم، انتشارات دانشگاه علم و صنعت ایران، 1380
[2] احد کاظمی، سیستم های قدرت الکتریکی جلد دوم، انتشارات دانشگاه علم و صنعت ایران، 1373
[3]علی کافی، کنترل، مرکز نشر دانشگاهی، 1370
[4] علی کافی، کنترل مدرن، مرکز نشر دانشگاهی، 1370
[5] IEEE Working Group Report, ”Hydraulic Turbine for System Dynamic Studies”, IEEE Trans. On Power Systems, Vol.7, No.1, February 1992, pp.167-179.
[6] IEEE PES Working Group,” Dynamic Models for Fossil Steam Units in Power Systems Studies “, IEEE Trans. On Power Systems, Vol 6, No.2, May 1991 Pp.753-761.
[7] N.S. Dhaliwal, H.E. Wichert “Analysis of PID Governors in Multi-machine System”, IEEE Trans. On Power Systems, Vol.PAS-97, No.2, pp456-463, March 1978
[8] P. Kundur, Power System Stability and Control, McGraw-Hill, 1994
[9] Moon YH et al,”Modified PID Loud-Frequency Control”, IEEE PES 1999 Winter Meeting, Feb.1999
[10] Moon YH et al, et al, ”Improvement of System Damping by Using the Differentia Feedback”, IEEE PES 1999 Winter Meeting, Feb.1999
[11] Cyme International INC., ”CYMSTAB Users Guide and reference Manual”, June, 1998
[12] Magdy E. Aboul-Ela, A.A.Fouad, “Damping Controller Design for Power System“, IEEE Trans. On Power Systems, Vol .11, May 1996, pp767-773
[13] M. Klein, G.j. Rojers, P. Kundur, ”A Fundamental Study of Inter-Area Oscillation in Power System”, IEEE Trans. PWRS., Vol 6, No.3, August, 1991, pp914-921
[14] Xiaoqing Yang, Ali Feliachi, “Stabilization of Inter-Area Oscillation Models Through Excitation System”، IEEE Trans. On Power Systems, Vol 9, No.1 ,Feb, 1994, pp494-502
[15] Kazofsky، L.G.، Turgeman, E “Non Reclusive Adaptive Impulse Noise Canceler, INT.J. CIRCUIT THEORY and APPLIC, Vol 10, No.3, pp231-242
حتما اگر تجربه ای یا نکته ای در مورد کنترل فرکانس بار در سیستم های قدرت دارید در قسمت دیدگاه ها مطرح کنید تا ماهم استفاده کنیم، سپاس.
راستی! برای دریافت مطالب جدید در کانال تلگرام PowerEn عضو شوید.







سلام. یه سوال دارم از خدمتتون. در یک واحد نیروگاهی وقتی بهره بردار قصد افزایش بار داشته باشد، با شارژ آب و گاز و هوا به بویلر و سپس فرمان دادن به گاورنر و به تبع آن، باز نمودن والوهای بخار و افزایش توان مکانیکی توربین این کار را انجام میدهد. پس از این کار توان خروجی ژنراتور افزایش پیدا میکند. حال سوال این است که: چگونه این اتفاق (افزایش توان خروجی ژنراتور) رخ میدهد بدون اینکه بهره بردار از نظر الکتریکی اقدامی کرده باشد؟!! به عبارتی چگونه هیچ پارامتر ورودی الکتریکی نداریم اما مگاوات خروجی افزایش می یابد؟! باسپاس… بیشتر »
سلام ممنون از مطالب آموزنده و خوبتون
امکانش هست فایل متلب سیستم دو ناحیه ای رو در اختیار من بذارید؟
با سلام وقت بخیر
در صورت امکان فایل ورد مقاله کنترل بار فرکانس ارسال بفرمایید
با تشکر
سلام
بنده نوشتم و فایل ورد نیست!
سلام و خسته نباشید
ضمن تشکر از مقاله خوب و جامع شما.
با اجازه، از مقاله به عنوان منبع برای پایان نامه استفاده کردم. اگر مشخصات رو برای ذکر در منابع بفرمایید ممنون میشم.
سلام
باعث خوشحالی هست، منابع انتهای مطلب هست اگر قصد ارجاع به این مقاله را دارید به این صورت ثبت کنید
محمد سیاهتیری، “کنترل فرکانس بار”، PowerEn، اردیبهشت ۱۳۹۹
سلام وقت بخیر،برای شبکه هایی که سیستم بادی هم در ان استفاده شده است،AGC به چه صورت است؟با تشکر
سلام
این مسئله در تمام شبکه استفاده میشه و البته فقط یک کنترل ساده نیست بلکه ترکیبی از متدهای مختلف در عمل پیاده سازی میشه
سوالتون خیلی کلی هست، اگر اصلا با AGC اشنا نیستید توصیه میکنیم یک مقاله ریوو در IEEE مطالعه بفرمایید