سیمولینک ماشین القایی 3 فاز
-
آپدیت شده در :

یکی از شبیه سازی های جالب با متلب؛ سیمولینک ماشین القایی 3 فاز هست که در آن به بررسی جریان های سه فاز استاتور، رتور، سرعت، گشتاور و در نهایت نمودار گشتاور – سرعت پرداخته می شود. موتور القایی که در این سیمولینک استفاده کرده ایم به صورت بلوک آماده نبوده بلکه به صورت کاملا غیرخطی طراحی شده است (علت این کار افزایش سطح علمی تمرین بوده است).
پیشنهاد ویژه
به شما پیشنهاد می کنیم حتما از آموزش سیمولینک متلب (جامع ترین آموزش شبیه سازی در نرم افزار متلب) دیدن نمایید.
همانگونه که می دانید هر ماشین الکتریکی در نرم افزار متلب دارای یک بلوک آماده است، ما برای افزایش سطح علمی تمرین امروز، از بلوک آماده برای موتور القایی سه فاز استفاده نکرده ایم بلکه طبق معادلات اثبات شده، به طراحی غیرخطی آن پرداخته ایم، منبع این طراحی مقاله ارائه شده با عنوان “”Transient Load Model of an Induction Machine”” و نوشته شده توسط “J.J.Cathey, R.K. Calvin and A.K. Ayoub” می باشد که می توانید از طریق وب سایت IEEE به آن دسترسی پیدا نمایید.
تمرین فوق یکی از شبیه سازی های(تمرین) کتاب “تحلیل ماشین های الکتریکی و سیستم های محرکه” نوشته: پال سی کراوز یا کراوس نیز می باشد، هر چند که این شبیه سازی در خیلی از کتاب های مهندسی دیگر نیز مورد استفاده قرار گرفته است.
در کنار سیمولینک شما می توانید موتور القایی 3 فاز را به صورت M فایل نیز کدنویسی نمایید، شاید در نگاه اول فهم “ام فایل” مشکل تر به نظر برسد اما در پروژه های سطح بالا مثل همین مورد، موتور القایی 3فاز(البته کامل طراحی شده از صفر نه بلوک آماده) فهم Mفایل به این دلیل که به صورت خط به خط نوشته و اجرا می گردد راحت تر است. در این تمرین جهت ایجاد تنوع قسمتی از خروجی ها را با Mفایل بدست آورده ایم.
توجه داشته باشید؛ که هر دو موتور (بلوک و M فایل) دقیقا یکی بوده، و در طراحی بلوک دیاگرامی برای شما ماسک نیز قرار داده ایم تا بتوانید متغیرهای ورودی را به سادگی با توجه به نیاز خوتان تغییر دهید.
نحوه تغییر موتور القایی 3 فاز و جایگزین کردن مقادیر خود را در ویدیو زیر توضیح داده ایم؛
شبیه سازی حالت بلوک دیاگرامی
موتوری که ما قصد طراحی آن را داریم یک موتور با توان 3hp (سه اسب بخار) می باشد که در جدول زیر مشخصات مربوط به آن را مشاهده می نمایید؛

در ابتدا موتور القایی 3 فاز را به صورت بلوک دیاگرامی طبق روابط ریاضی آن طراحی می کنیم که در زیر تصویر آن قرار داده شده است.
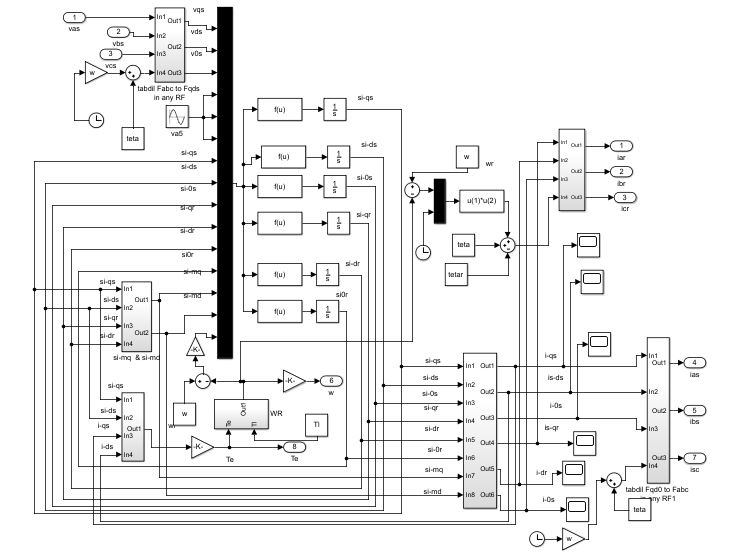
در نهایت با توجه به ورودی های لازم این بلوک، آن را به 4 بلوک ویژه سیگنال ورودی متصل می کنیم و از سمت دیگر 7 خروجی که شامل جریان های سه فاز استاتور، جریان های سه فاز رتور و سرعت موتور می باشد متصل می کنیم.
در نهایت تصویر زیر کل پروژه ما را نشان می دهد؛
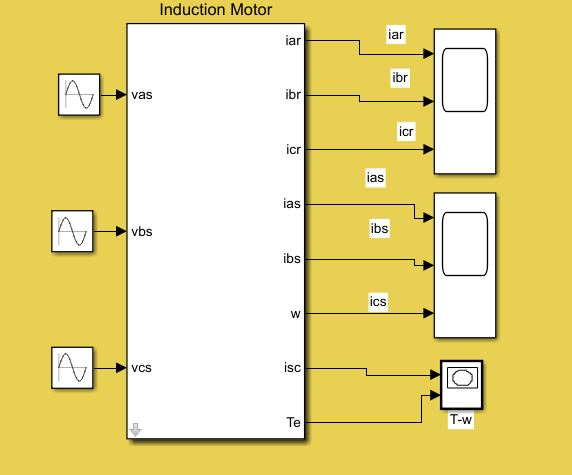
البته در نظر داشته باشید که ما هیچ یک از عوامل تلف زا مانند؛ اصطحکاک، مقاومت هوا و … را در نظر نگرفته ایم.
تحلیل حالت بلوک دیاگرامی
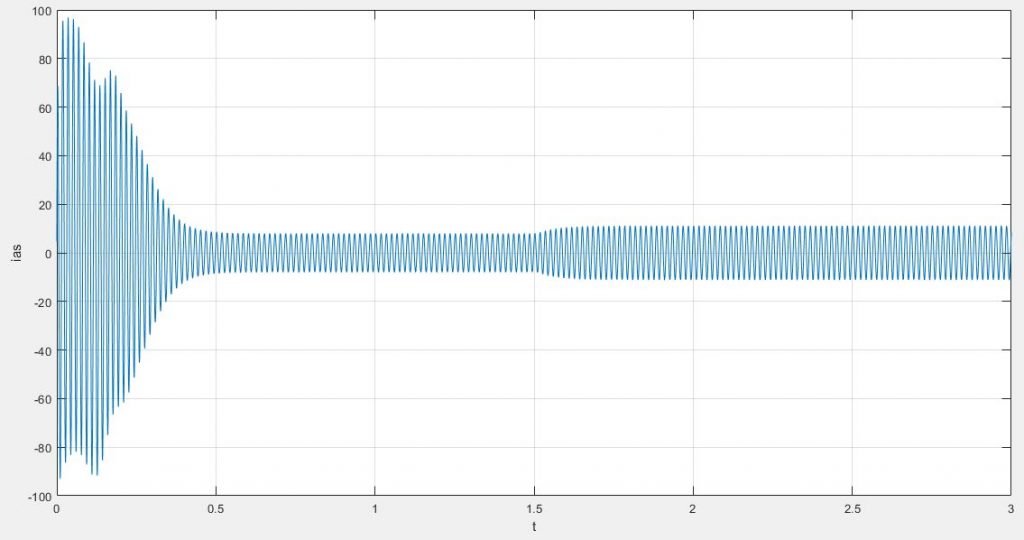
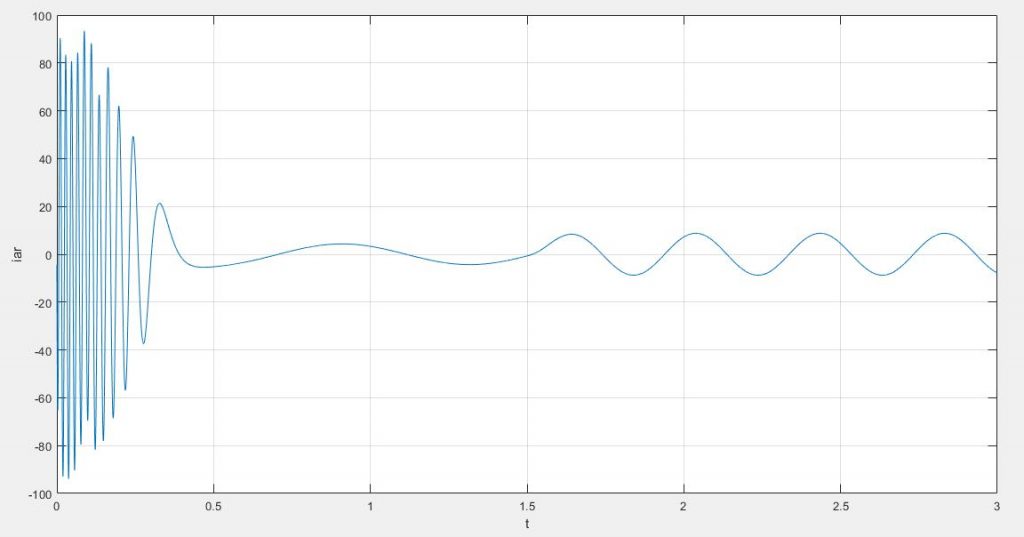
همانگونه که در نمودار های زیر مشاهده می کنید برخلاف تصور نوسانات جریان های استاتور بیشتر از رتور بوده و حتی در زمان میرا شدن هم شاهد تفاوت زیادی بین این دو جریان هستیم؛ به گونه ای که جریان های رتور نسبت به استاتور زودتر میرا شده اند.
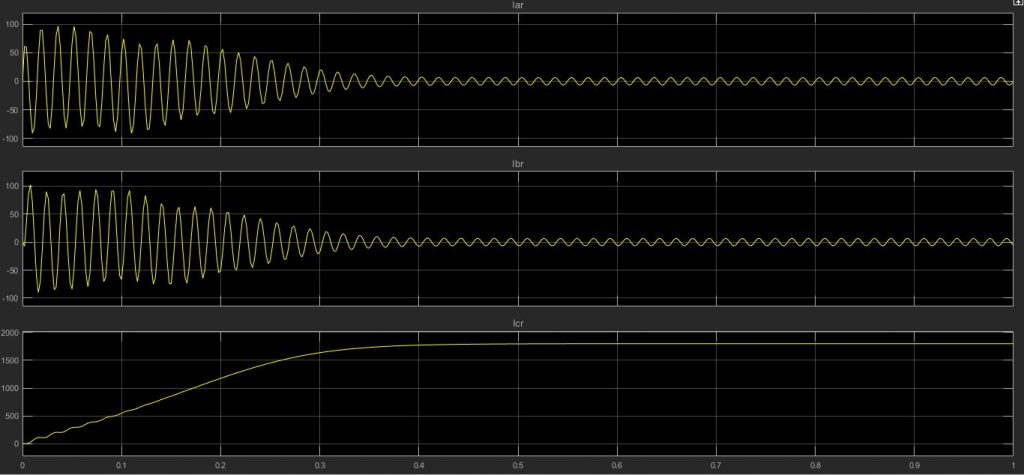
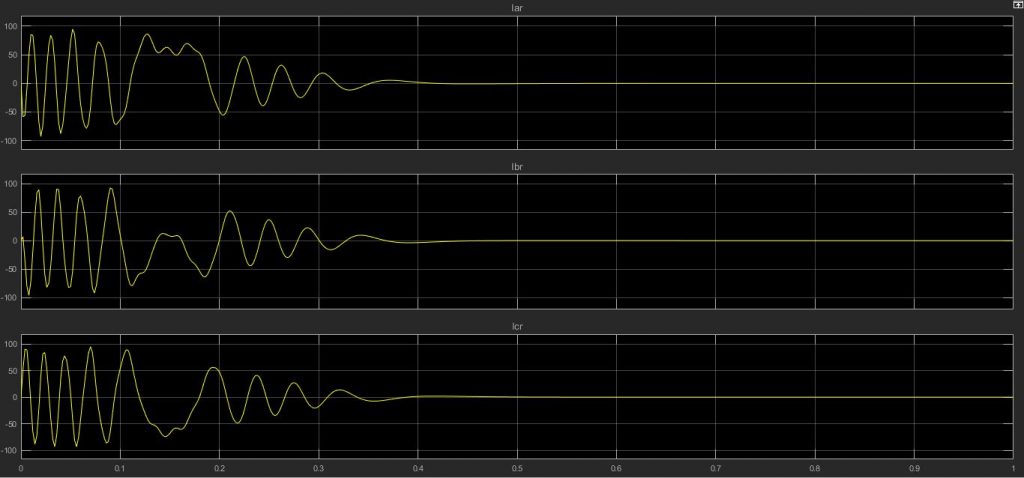
شبیه سازی موتور با M فایل
با توجه به اینکه ماشین های القایی با توان پایین(3hp) دارای لغزش نسبتا بالایی هستند و به همین دلیل گشتاور نامی در سرعتی خیلی کمتر از سرعت نامی ظاهر می شود قصد داریم با شبیه سازی این موتور این مطلب را در قالب نمودار مشاهده(اثبات) نماییم، و ببینیم در چه سرعتی شاهد گشتاور نامی خواهیم بود.
پس در ابتدا شروع به وارد کردن داده های موتور القایی به صورت زیر می نماییم، توجه داشته باشید که این موتور دقیقا همان موتور شبیه سازی شده در قسمت قبلی می باشد؛
clear all clc J=.089; rr=.816; t=0; i=0; dt=.0001; P=4; Tl=11.9/2; Te=0; tet0=0;tetr0=0;tet=0;tetr=0; rs=.435; Wr0=0; Xlr=.754; Xls=.754; Wb=120*pi; Xm=26.13; Xss=Xls+Xm; Xrr=Xlr+Xm;
و سپس طبق معادلات بیان شده برای ماشین القایی به صورت غیرخطی عمل می کنیم و روابط ریاضی را به صورت ماتریسی می نویسیم که در زیر آورده شده اند؛
D=(Xss*Xrr)-(Xm^2);
vqr=0;vdr=0;vor=0;
Q0=[0;0;0;0;0;0];
Qqs=0;Qds=0;Qos=0;Qqr=0;Qdr=0;Qor=0;
while t<=3 Vas=220*(.8165)*cos(Wb*t); Vbs=220*(.8165)*cos((Wb*t)-(2*pi/3)); Vcs=220*(.8165)*cos((Wb*t)+(2*pi/3)); Ks=(2/3)*[cos(tet0) cos((tet0)-(2*pi/3)) cos((tet0)+(2*pi/3));sin(tet0) sin((tet0)-(2*pi/3)) sin((tet0)+(2*pi/3));.5 .5 .5]; V1=Ks*[Vas;Vbs;Vcs]; vqs=V1(1,1);vds=V1(2,1);vos=V1(3,1); Q=[Qqs;Qds;Qos;Qqr;Qdr;Qor]; V=[vqs;vds;vos;vqr;vdr;vor]; Wr=Wr0; W=Wr; A=[rs*Xrr/D (W/Wb) 0 (-rs*Xm/D) 0 0;(-W/Wb) rs*Xrr/D 0 0 -rs*Xm/D 0;0 0 rs/Xls 0 0 0;-rr*Xm/D 0 0 rr*Xss/D (W-Wr)/Wb 0;0 (-rr*Xm/D) 0 (-(W-Wr)/Wb) rr*Xss/D 0;0 0 0 0 0 rr/Xlr]; B=[1/Wb 0 0 0 0 0;0 1/Wb 0 0 0 0;0 0 1/Wb 0 0 0;0 0 0 1/Wb 0 0;0 0 0 0 1/Wb 0;0 0 0 0 0 1/Wb]; Brev=inv(B); Arev=-inv(B)*A; Q01=Arev*Q+Brev*V; Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))-(Q(2,1)*Q(4,1))); Wr01=(P/2)*((Te-Tl)/J); tet01=W; tetr01=Wr; Wr=Wr0+(Wr01*dt/2); tet=tet0+(tet01*dt/2); tetr=tetr0+(tetr01*dt/2); Q=Q0+(Q01*dt/2); Q02=Arev*Q+Brev*V; Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))-(Q(2,1)*Q(4,1))); Wr02=(P/2)*((Te-Tl)/J); Wr=Wr0+(Wr02*dt/2); W=Wr; tet02=W; tetr02=Wr; tet=tet0+(tet02*dt/2); tetr=tetr0+(tetr02*dt/2); Q=Q0+(Q02*dt/2); Q03=Arev*Q+Brev*V; Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))-(Q(2,1)*Q(4,1))); Wr03=(P/2)*((Te-Tl)/J); Wr=Wr0+(Wr03*dt); W=Wr; tet03=W; tetr03=Wr; tet=tet0+(tet03*dt); tetr=tetr0+(tetr03*dt); Q=Q0+(Q03*dt); Q04=Arev*Q+Brev*V; Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))-(Q(2,1)*Q(4,1))); Wr04=(P/2)*((Te-Tl)/J); Wr0=Wr0+(Wr01+2*Wr02+2*Wr03+Wr04)*(dt/6); W=Wr0; tet04=W; tetr04=Wr; tet0=tet0+(tet01+2*tet02+2*tet03+tet04)*(dt/6); tetr0=tetr0+(tetr01+2*tetr02+2*tetr03+tetr04)*(dt/6); Q0=Q0+(Q01+Q02*2+2*Q03+Q04)*(dt/6); Qqs=Q0(1,1);Qds=Q0(2,1);Q0s=Q0(3,1);Qqr=Q0(4,1);Qdr=Q0(5,1);Q0r=Q0(6,1); Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))-(Q(2,1)*Q(4,1))); I=(1/D)*[Xrr 0 0 -Xm 0 0;0 Xrr 0 0 -Xm 0;0 0 D/Xls 0 0 0;-Xm 0 0 Xss 0 0;0 -Xm 0 0 Xss 0;0 0 0 0 0 D/Xlr]*Q; iqs=I(1,1);ids=I(2,1);ios=I(3,1);iqr=I(4,1);idr=I(5,1);ior=I(6,1); Kr=(2/3)*[cos((tet0-tetr0)) cos(((tet0-tetr0))-(2*pi/3)) cos(((tet0-tetr0))+(2*pi/3));sin((tet0-tetr0)) sin(((tet0-tetr0))-(2*pi/3)) sin(((tet0-tetr0))+(2*pi/3));.5 .5 .5]; Irotor=inv(Kr)*[iqr;idr;ior]; iar=Irotor(1,1);ibr=Irotor(2,1);icr=Irotor(3,1); Ks=(2/3)*[cos(tet0) cos((tet0)-(2*pi/3)) cos((tet0)+(2*pi/3));sin(tet0) sin((tet0)-(2*pi/3)) sin((tet0)+(2*pi/3));.5 .5 .5]; Istator=inv(Ks)*[iqs;ids;ios]; ias=Istator(1,1);ibs=Istator(2,1);ics=Istator(3,1); i=i+1; time(i)=t; Iar(i)=iar; Tee(i)=Te; Ias(i)=ias; WW(i)=(30*Wr0)/(2*pi); t=t+.0001; if t>=1.5
Tl=11.9;
end
endدر ادامه از دستور plot استفاده کرده و خروجی های مدنظر را ترسیم می نماییم؛
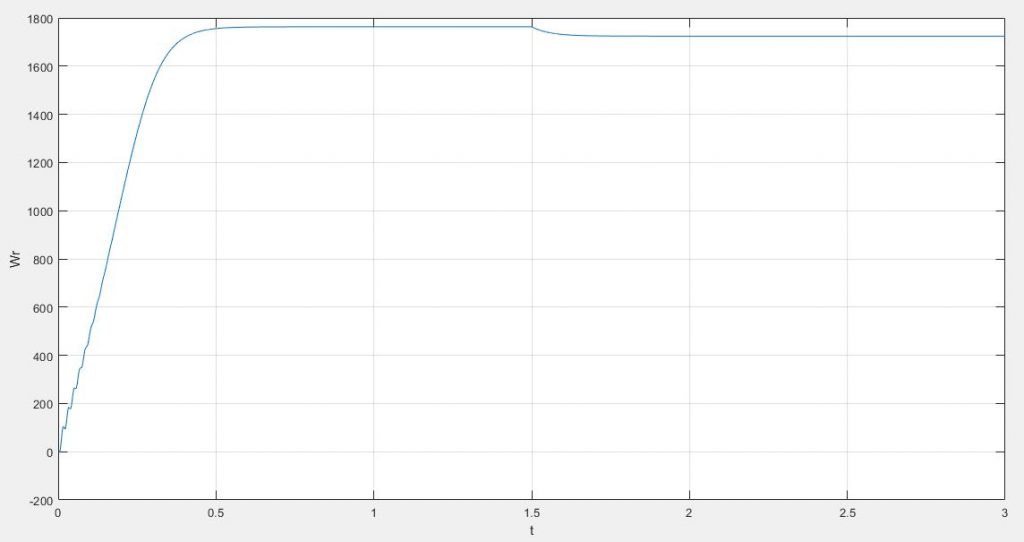
plot(time,WW);xlabel('t') ;ylabel('Wr')
grid on
figure
plot(time,Ias);xlabel('t') ;ylabel('ias')
grid on
figure
plot(time,Iar);xlabel('t') ;ylabel('iar')
grid on
figure
plot(time,Tee);xlabel('t') ;ylabel('Te')
grid on
figure
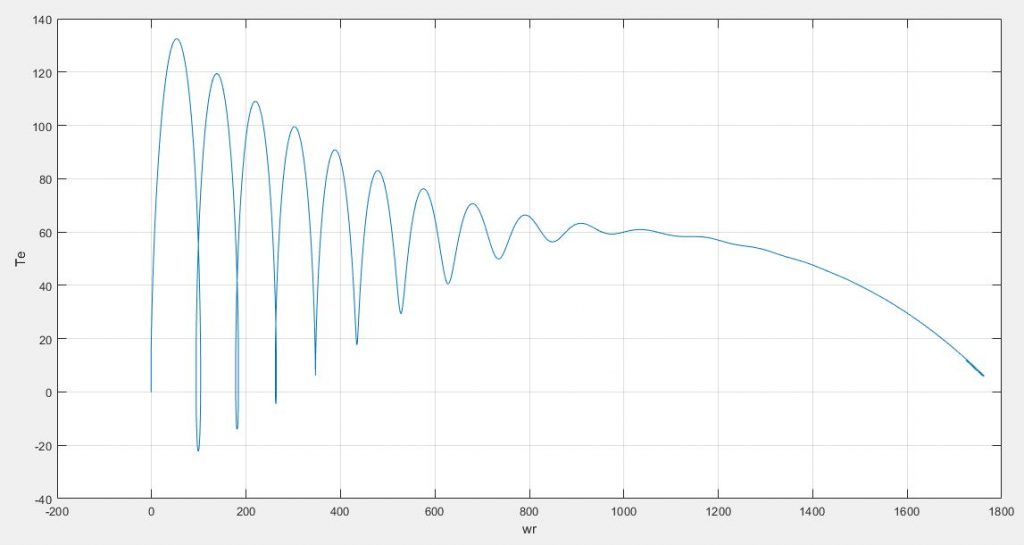
plot(WW,Tee);xlabel('wr') ;ylabel('Te')
grid on
تحلیل شبیه سازی حالت M فایل
قاعدتا انتظار ناحیه گذرا را داریم، و شاید در نگاه اول انتظار تاثیر حالت گذرا بروی جریان های استاتور که به شبکه سه فاز متعادل متصل است را نداشته باشیم، و بیشتر انتظار نوسانات شدید را بروی رتور داشته باشیم.
در برنامه ای که نوشته ایم در ابتدا از موتور خواسته ایم که به سرعت پایدار خود بدون بارداری برسد که توانسته در سرعت 1763.1 به پایداری مد نظر برسد.
همانگونه که می بینید در این حالت بدلیل استارت از حالت سکون شاهد بیشترین نوسانات در جریان استاتور، جریان رتور و گشتاتور هستیم.
از طرفی به دلیل پایین بودن توان ماشین (3hp)؛ موتور در سرعت کمتری به گشتاور نامی رسیده است(لغزش بالاست) با دقت در نمودار گشتاور – سرعت، در سرعت 1000rpm موتور به گشتاور نامی خود رسیده است.
مطالب بیان شده در نمودار های زیر قابل مشاهده هستند؛
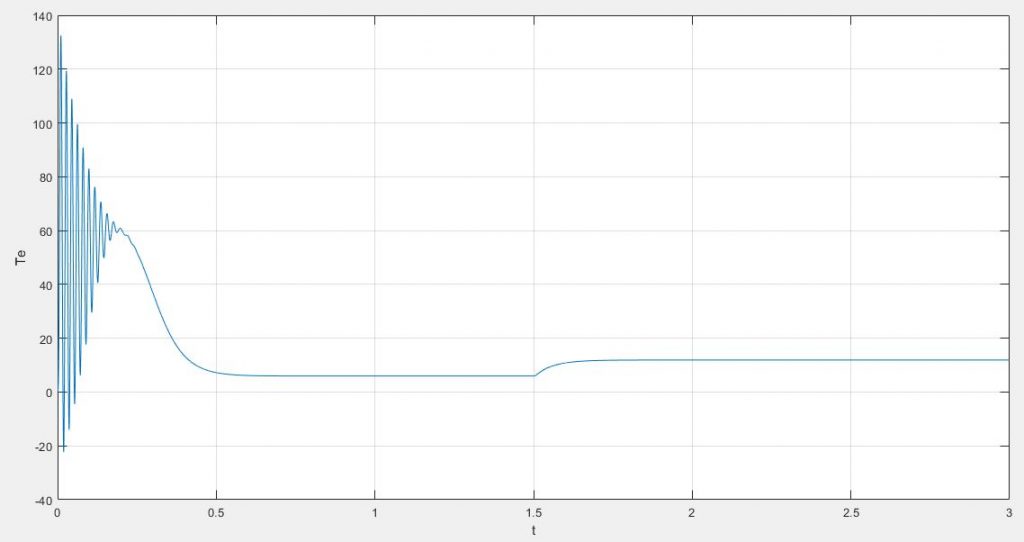
در ادامه در زمان 1.5 ثانیه به موتور یک بار متصل کرده ایم که در جریان استاتور و رتور تاثیر گذاشته و عملا باعث افزایش جریان عبوری در استاتور شده است، از طرفی نیز باعث افزایش و ایجاد هارمونیک در جریان های رتور نیز گشته است.
مورد دیگر گشتاور راه اندازی موتر القایی می باشد که با توجه به نوسانی بودن آن(صرف نظر از این مورد) گشتاور راه اندازی خوبی ایجاد کرده است که یکی از محاسن این نوع موتور نیز می باشد(البته همچنان موتور های DC در این زمینه بی رقیب هستند).
 دانلود مستقیم فیلم توضیحات سیمولینک ماشین القایی 3 فاز – HD | با حجم 11 مگابایت
دانلود مستقیم فیلم توضیحات سیمولینک ماشین القایی 3 فاز – HD | با حجم 11 مگابایت
 دانلود مستقیم فایل شبیه سازی موتور القایی 3 فاز – بلوک دیاگرامی | با حجم 1 مگابایت
دانلود مستقیم فایل شبیه سازی موتور القایی 3 فاز – بلوک دیاگرامی | با حجم 1 مگابایت
 دانلود مستقیم فایل شبیه سازی موتور القایی 3 فاز – M فایل | با حجم 1 مگابایت
دانلود مستقیم فایل شبیه سازی موتور القایی 3 فاز – M فایل | با حجم 1 مگابایت
![]() پسورد : www.poweren.ir
پسورد : www.poweren.ir
راستی! برای دريافت مطالب جديد در پیج اینستاگرم PowreEn عضو شويد.







سلام
توضیحات کد های ام فایل این پروژه رو چطور می تونم تهیه کنم؟
تشکر
سلام . داخل نمودار ias و iar و wr مخفف چی هست؟
جریان استاتور،جریان روتور، سرعت روتور
سلام فایل سیمولینک slx در داخل قسمت دانلود مستقیم فایل شبیه سازی موتور القایی 3 فاز – بلوک دیاگرامی | با حجم 1 مگابایت وجود ندارد!!!
سلام
ام فایل هست و حجمش کمتر از یک مگ هست
سلام خسته نباشید من چجوری میتونم فیلم صفر تا صد این طراحی رو داشته باشم میخوام خودم اینو توسیمولینک کار کنم وبدونم چرا از این بلوک ها استفاد ه میکنیم چرا بلوک دیگی استفاد نمیکنیم خلاصه من تازه شروع کردم شبیه سازی تو محیط متلب رو اگه ممکنه فیل یا فایل های که واسه یادگیری کمک میکنه واسه من معرفی کنید ممنون میشم
سلام
بله خیلی مسائل هستند که نمیشه اینجا توضیح داد ولی با دوره ۰ تا ۱۰۰ سیمولینک متلب همه این موارد رو خواهید آموخت
با سلام
فایل شبیه سازی سیمولینک در لینک مورد نظر موجود نیس چرا؟ منظور پسوند Slx هستش
سلام
این ام فایل هست طبق اموزش جلو برید
سلام.میتونیم به این شبیه بار وصل کنیم”؟مثل ویسکوز یا ترکشن
سلام
نه با این جزئیات